Lieu inhabité

[geometrodynamics_of_QFT]

S'i ne s'agit que d'un problème d'homothétie de rapport 2, alors les angles alpha et theta sont égaux, et le point C' est sur la droite (FF').

Ok, je comprends bien ce que vous voulez dire...
Mais si c'est effectivement le cas...il faut pourtant bien que l'abscisse du point C' tende vers 1/2 lorsque tend vers non? (puisque P'' tend vers (1,1) et que la médiatrice de [F'P''] passant par C' est verticale...)
-----

[geometrodynamics_of_QFT]

Pour moi, le lieu des points C' serait effectivement sur la droite verticale x=1 SI l'axe F'P'' (perpendiculaire à l'axe de la 2ème projection stéréographique par le cercle mauve) restait horizontal.
Or, il passe de vertical à horizontal au cours de la transformation, ce qui diffère de l'axe de la première projection (par le cercle noir de rayon 1/2), qui lui reste horizontal du début à la fin!

Enfin, mon argument principal:
la distance entre le point C' et le milieu du segment [F'P''] est égale à simplement la tangente de l'angle alpha, multipliée par le diamètre du cercle mauve, càd 1/2. (de la même manière que le point C est à une distance tangente theta du milieu du segment [FF'])
Or, si le point C' était sur l'axe des ordonnées x=0, le triangle C'F'P'' serait isocèle ([C'F'] et [C'P''] étant les rayons)
Mais dans ce cas, l'angle alpha = angle[F'P''C'] est effectivement égal à l'angle theta = angle[C'F'P''].
Donc le dernier angle (qu'on appelera =angle[F'C'P'']) du triangle C'F'P''est égal à .
Mais cet angle est également égal à en comptabilisant la somme des angles du triangle rectangle formé par:
- l'axe x=0
- le segment [F'P'']
- la médiatrice du segment [F'P'']

Donc .
Ce qui aboutit à une contradiction.

[geometrodynamics_of_QFT]

Bonjour, je passe par là, projection stéréographique : https://www.youtube.com/watch?v=05eQLnxsTd0.
tu 'as dessiné tous sur un seul plan ????

moi non plus je ne comprends pas. Peut-être que si tu expliquais l'origine de ce problème on comprendrait.

Merci pour le lien.
Oui donc il s'agit bien de projections stéréographiques, le but de ce fil est d'en étudier des propriétés de manière plus profonde.
On considère ici la projection stéréographique en 2D (donc un cercle au lieu d'une sphère), pour justement ne pas s'embrouiller inutilement d'une dimension spatiale supplémentaire, qui ne change fondamentalement rien à la nature des relations géométriques ici à l'oeuvre.
Toute contribution concernant le lieu des pointc C' est plus que la bienvenue!!!
Merci

@minushabens : le but dans un premier temps de l'exercice, est de trouver le lieu des points C' : centres situés sur la médiatrice de [F'P''] des cercles passant par F' et P''.
Ensuite, trouver où converge l'itération de ce processus par exemple...je ne sais pas encore..

[azizovsky]

non, il y'a une différence entre 2 et 3 dimensions, car moi je vois des cercle au lieu des segment...., dans n'importe quelle position de p'', tu divise en deux [F'P''] pour construire ton cercle mauve, dans tous les cas, ton cercle a un rayon fixe, un cercle qui roule dans un cercle, C' parcourt le cercle de centre F' et de rayon F'G s'elle appartient au cercle mauve (l'ange alpha =0), dans les autre cas, il décrit un arc de cercle .

[geometrodynamics_of_QFT]

non, il y'a une différence entre 2 et 3 dimensions, car moi je vois des cercle au lieu des segment...., dans n'importe quelle position de p'', tu divise en deux [F'P''] pour construire ton cercle mauve,

Je vous remercie grandement pour votre remarque.

dans tous les cas, ton cercle a un rayon fixe, un cercle qui roule dans un cercle

Oui, le cercle mauve est fixe tout au long du parcours, ses dimensions ne changent pas. C'est l'équivalent du cercle de rayon 1/2 centré en G qui intervient dans la 1ère projection stéréographique (du point P vers le point P' sur l'axe x)

C' parcourt le cercle de centre F' et de rayon F'G s'elle appartient au cercle mauve (l'ange alpha =0), dans les autre cas, il décrit un arc de cercle .

Bien que C' parte du point G lorque , on voit que son ordonnée tend vers -l'infini lorsque tends vers [/TEX]\pi/2[/TEX].
Le lieu de ces points C' ne peut doncpas se situer sur un arc de cercle de rayon constant au cours de la transformation...

Je me trompe?

Voilà une nouvelle illustration reprenant les éléments importants pour trouver ce lieu :



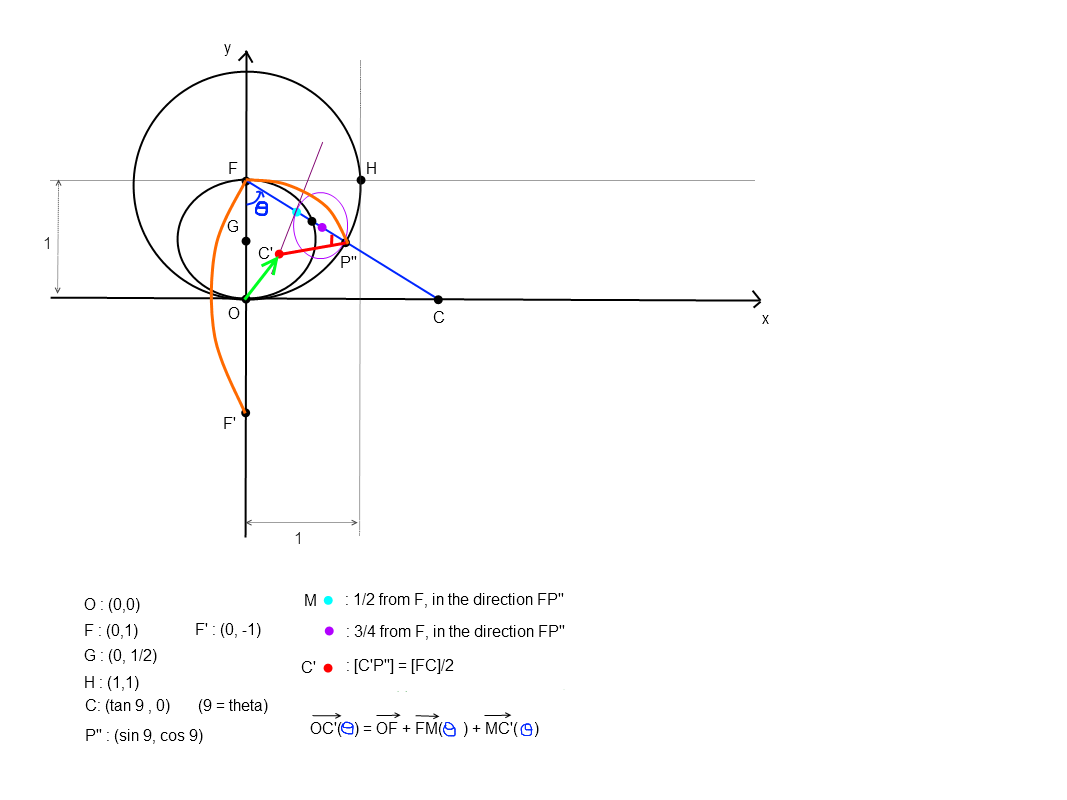
On va bien voir directement, dans mon prochain post, qui a raison, étant donné que je m'aprette à obtenir l'expression du vecteur dans le repère (x,y).

[azizovsky]

Je vous remercie grandement pour votre remarque.


Oui, le cercle mauve est fixe tout au long du parcours, ses dimensions ne changent pas. C'est l'équivalent du cercle de rayon 1/2 centré en G qui intervient dans la 1ère projection stéréographique (du point P vers le point P' sur l'axe x)


Bien que C' parte du point G lorque , on voit que son ordonnée tend vers -l'infini lorsque tends vers [/TEX]\pi/2[/TEX].
Le lieu de ces points C' ne peut doncpas se situer sur un arc de cercle de rayon constant au cours de la transformation...
.

oui, par projection stéréographique sur l'axe des x quand l'angle (alpha) est égale à 0, dans les autre cas non: grand mais fini (x< l'infini).
dans quel repère tu veux définir ton point ?

[geometrodynamics_of_QFT]

DONC:








Mais dans le triangle rectangle C'MP'' (angle droit en M), l'hypoténuse [C'P''] est le rayon de l'arc entre F et P'', et vaut donc la moitié du rayon de l'arc entre F et F', qui lui vaut simplement [F'C] càd .

Donc on peut écrire cette égalité de longueur de segment [C'P''] par :



Donc :

!

quid God's heart?

[geometrodynamics_of_QFT]

Donc en poursuivant :



Donc

toujours avec

Est-ce correct?

[azizovsky]

puisque le point C'' est à égale distance de P'' et F', dans n'importe quelle position de P'' , il garde cette propriété, donc l'angle est constante (ne dépend pas de )

[geometrodynamics_of_QFT]

Ce qui donnerait :



après simplifications.
toujours correct?

Quelqu'un connait-il un endroit en ligne où on peut plotter ce genre de courbe paramétrique?

[geometrodynamics_of_QFT]

puisque le point C'' est à égale distance de P'' et F', dans n'importe quelle position de P'' , il garde cette propriété, donc l'angle est constante (ne dépend pas de )

à égale distance ne veut pas dire proche. En l'occurence, quand theta tend vers pi/2, cette distance est énorme, et bien en bas dans le graphe...non?

[geometrodynamics_of_QFT]

Voilà!!! eureka!!

donc en exprimant theta en fonction de x dans l'expression pour y(theta), on trouve:


j'ai le lieu! Et il est bien inhabité :


Et la courbe ressemble à ce que j'avais pressenti!!!
Et quelle est cette racine? 0.2etc. ????

[azizovsky]

à égale distance ne veut pas dire proche. En l'occurence, quand theta tend vers pi/2, cette distance est énorme, et bien en bas dans le graphe...non?

quel repère ? (mieux encore, indépendante du dessinateur , moi je la dessine à ).les points F,P''(on parle deux langages différents....)

[geometrodynamics_of_QFT]

un zoom sur la racine de F(x) :

[geometrodynamics_of_QFT]

quel repère ? (mieux encore, indépendante du dessinateur , moi je la dessine à ).les points F,P''(on parle deux langages différents....)

repère (x,y) du dessin du message #35.
Restons dans le plan réel (géométrie euclidienne), est-ce possible?

[geometrodynamics_of_QFT]

Toujours le même lieu, la même courbe, d'un autre point de vue:


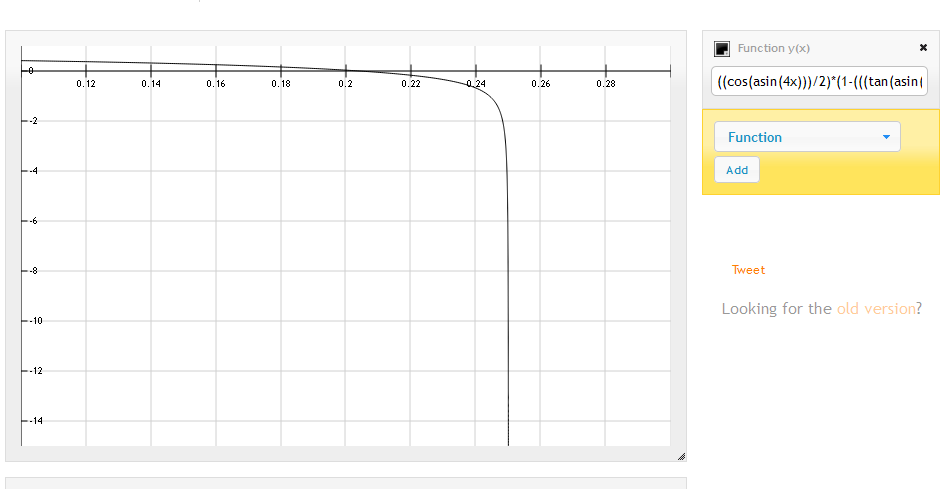
La descente est tellement raide que la courbe s'arrête en y=~-150, avec une valeur qui est toujours proche de 0.25.
(Alors que la courbe est censé avoir une asymptote en x=0.5..n'est-ce pas?)
Vue de plus loin encore, c'est presqu'un angle droit...
Des cercles partout et soudain...un angle droit...

[azizovsky]

repère (x,y) du dessin du message #35.
Restons dans le plan réel (géométrie euclidienne), est-ce possible?

comme carreleur, je part d'un point pratique...

[geometrodynamics_of_QFT]

Et puisque cos (asin x) = sqrt(1-x²) et que tan (asin x) = x / sqrt(1 - x²) :

On ré-algébrise F(x) en :


ou encore :



Quelqu'un peut-il confirmer la justesse de tous ces calculs svp?

[geometrodynamics_of_QFT]

comme carreleur, je part d'un point pratique...

Et de quel point partez-vous?
Je pars moi du point (0,0), nommé O sur le dessin, côté pratique...

Le point C' quand theta = 0 est le point (0,1/2) dans ce repère.

[azizovsky]

ok,

j'ai le lieu! Et il est bien inhabité

regarde est ce qu'il est carrelé ? .

[geometrodynamics_of_QFT]

La racine de F(x), F(x=R)=0, est alors :

[geometrodynamics_of_QFT]

ok,regarde est ce qu'il est carrelé ? .

lol, c'est quoi votre point au final?

quel voulez-vous dire explicitement, et pas avec des paraboles...?
J'aimerais avancer...

[azizovsky]

lol, c'est quoi votre point au final?

quel voulez-vous dire explicitement, et pas avec des paraboles...?
J'aimerais avancer...

sans arrière pensée..., car je me suis rendu compte que je n'est rien pigé dans ton problème: on cherchait à relier deux variables, or ce n'était pas le cas, le problème a été déplacé..., des fonctions que je ne sais pas d'où elles sortent..., donc j'ai quitté les lieux pour laisser la place au autres (je sais mes limites...).

[geometrodynamics_of_QFT]

on cherchait à relier deux variables, or ce n'était pas le cas, le problème a été déplacé...,

De quelles variables parlez-vous? si ce sont les angles et , le lien a été trouvé dans le message #37.

des fonctions que je ne sais pas d'où elles sortent

De quelle fonction parlez-vous?
S'il s'agit de la fonction F(x), il s'agit du lieu des points C' exprimé en terme d'une equation y=F(x), comme il l'a été défini dans le tout premier message #1 de ce fil (F(x) en turquoise)

..., donc j'ai quitté les lieux pour laisser la place au autres (je sais mes limites...).

J'entrevois en effet vos limites.

Pour la Nième fois : il s'agi(ssai)t de trouver le lieu formé par les points C' LORSQUE VARIE DE 0 à PI/2! (chaque valeur de theta fournit un point C' différent)

[azizovsky]

J'entrevois en effet vos limites.

en effet, un diplôme en physique théorique, j'ai passé par deux ans de MP.....

[geometrodynamics_of_QFT]

en effet, un diplôme en physique théorique, j'ai passé par deux ans de MP.....

Partez si voux ne voulez pas discuter de maths et du problème relatif à ce fil. Je me fous du reste, j'ai créé ce fil pour des maths, pas pour des gamineries. On a tous des diplômes, mais contrairement à vous, ils ne me limitent pas. Merci de votre compréhension. N'intervenez plus si ce n'est pas en lien avec le problème mathématique svp.

[azizovsky]

Partez si voux ne voulez pas discuter de maths et du problème relatif à ce fil. Je me fous du reste, j'ai créé ce fil pour des maths, pas pour des gamineries. On a tous des diplômes, mais contrairement à vous, ils ne me limitent pas. Merci de votre compréhension. N'intervenez plus si ce n'est pas en lien avec le problème mathématique svp.

ok, du calme geometrodynamics_of_QF, je n'ai rien dit, mon domaine, c'est le carrelage.(ça m'a fait plaisir de secouer mes neurones avec toi...) bonne soirée.

[geometrodynamics_of_QFT]

ok, du calme geometrodynamics_of_QF, je n'ai rien dit, mon domaine, c'est le carrelage.(ça m'a fait plaisir de secouer mes neurones avec toi...) bonne soirée.

Reprends aux quelques dernières pages de ce fil si tu ne comprends toujours pas, il y a des schémas en couleur. (à partir du post #153, où débute la discusison sur le lieu, dessin dans #172 : cercles oranges pour la valeur dessinée de theta, cercles rouges pour theta=0, "cercles" jaunes pour theta=pi/2)
Mais le contenu de ce fil-ci est censé être "self-contained", ou je ne sais plus comment on dit.
Toutes les infos y sont pour arriver à l'expression de F(x).

[azizovsky]

sans projection st, si C'' appartient au cercle mauve (cas particulier mais vérifie tous...C''=M), on pose :


on'a :

(formules d'Al Kashi dans le triangle OMF')

pour --> M(x,1)

?ce qui est évident...

dans les autres cas à demain (saturé)

[azizovsky]

sans projection st, si C'' appartient au cercle mauve (cas particulier mais vérifie tous...C''=M), on pose :


on'a :

(formules d'Al Kashi dans le triangle OMF')

pour --> M(x,1)

?ce qui est évident...

dans les autres cas à demain (saturé)

je n'est rien dit pour b ...à demain .pour