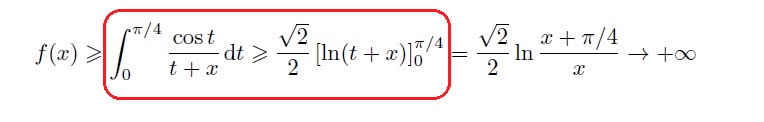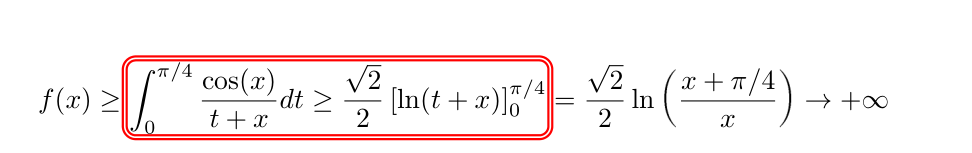Fonction non intégrable.. comment on est arrivé à l'inégalité?
Discussions similaires
-
Par inviteb4466a8c dans le forum Mathématiques du supérieur
Réponses: 17
Dernier message: 22/12/2014, 19h09
-
Par invite282d0678 dans le forum Mathématiques du supérieur
Réponses: 7
Dernier message: 24/10/2012, 18h05
-
Par invitef39e86ba dans le forum Mathématiques du supérieur
Réponses: 3
Dernier message: 12/10/2009, 17h56
-
Par Seirios dans le forum Mathématiques du supérieur
Réponses: 11
Dernier message: 14/08/2009, 11h32
-
Par invitea87a1dd7 dans le forum Mathématiques du supérieur
Réponses: 11
Dernier message: 02/03/2006, 17h10