Treilli additif

[invite4308cf33]

Bonjour.

Dans mon cours, on a une feuille de plusieurs treillis de différents groupes (Z/nZ, +) que j'ai joint à mon poste.

ATTENTION : sur le dessin il est écrit (Z/12Z, +) alors qu'il s'agit de (Z/10Z,+) (case en haut à droite !!)

Je n'arrive pas à les comprendre.

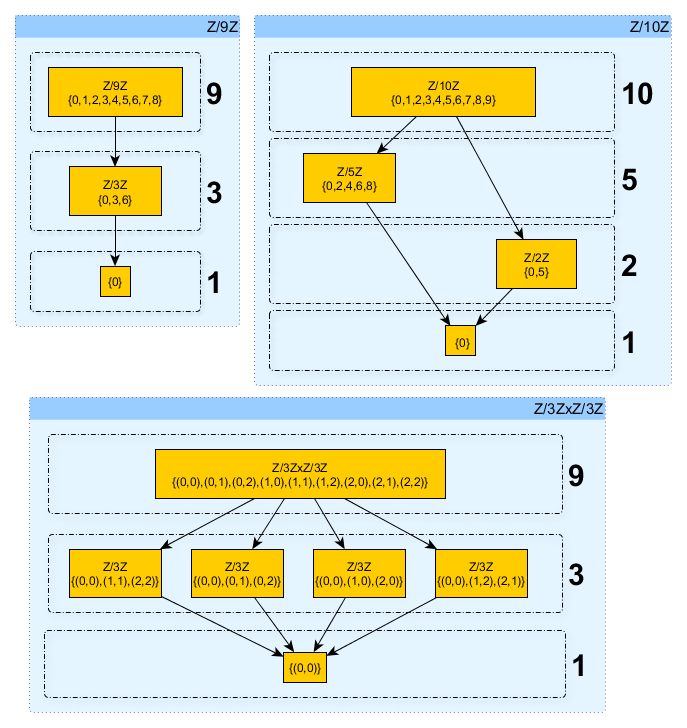
Pour (Z/9Z,+) les éléments sont d'ordre 1, 3 et 9. Jusqu'ici, OK.
On a 0 d'ordre 1 (l'élément neutre).
1, 2, 4, 5 et 7 d'ordre 9.
3 et 6 d'ordre 3.

Je comprends ce treilli (sauf les "1", "2" et "3" à l'intérieur des carrés).

Pour (Z/10Z, +), même schéma, sauf que le "groupe d'éléments d'ordre 2" n'a pas de lien direct avec celui d'ordre 5 (comment on pourrait dire ça de manière claire ?)

Mais alors les deux autres, c'est-à-dire (Z/3Z²,+) et (Z/2Z² x Z/3Z, +), je ne les comprends vraiment pas.

Pour (Z/3Z²), j'écris Z/3Z x Z/3Z.
Ici, je ne comprends donc pas pourquoi les éléments sont d'ordre 1, 3 et 9. Il me semblait que dans ce genre de produit cartésien, l'ordre des éléments (en l'occurrence) devait être d'ordre 1 ou 3...
Mais admettons...
Je compte un élément d'ordre 1, 4 éléments d'ordre 3 et 4 éléments d'ordre 9.
Pourquoi alors cet agencement ? Pourquoi mettre 4 carrés à "ordre 3" et 1 seul carré à "ordre 9" ?

D'ailleurs pour (Z/9Z, +), je ne comprends pas non plus pourquoi il y a qu'un seul carré de chaque alors qu'on compte, par exemple 5 éléments d'ordre 9 !!!

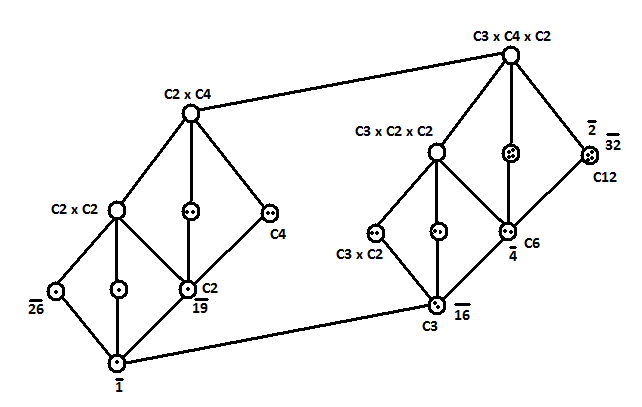
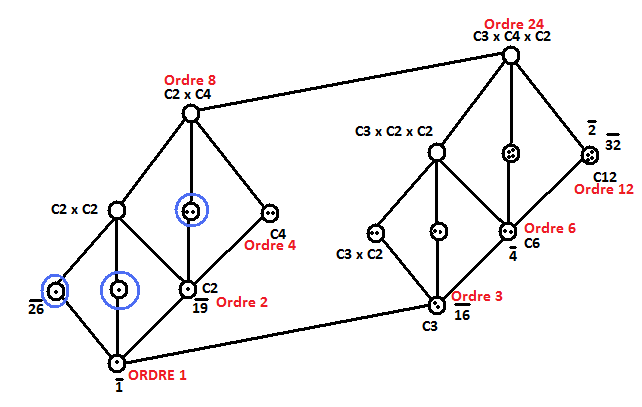
Et pour le dernier (Z/2Z² x Z/3Z, +), je ne le comprends encore moins (pourquoi les "fils" sont liés de cette façon ? etc), mais avant de m'y aventurer j'aimerais déjà comprendre l'essentiel de ces trois premiers...

Voici le lien joint :
-----

[Tryss2]

Étrange cette version, les chiffres dans les carrés n'ont aucun sens.

Les carrés ne représentent pas des éléments, mais des sous groupes ! Le chiffre à gauche donne l'ordre des sous groupes sur ce niveau et la flèche veut dire "est un sous groupe de"

Voici une version que j'espère plus claire des 3 premiers treillis :

[invite4308cf33]

Wow, alors là c'est on ne peut plus clair ! J'ai vraiment bien compris la notion de treillis ainsi que celle des sous-groupes. Vraiment, un grand merci pour ces images très très claires !
Je vais tenter de refaire le dernier treillis de cette façon

[invite4308cf33]

Rebonjour,

Pour les treillis additifs, j'ai parfaitement compris.
Mais si je dois dessiner le treillis de (Z/45Z)*, je me demande comment je dois procéder pour le construire.

On écrit (Z/45Z)* = (Z/5Z)* x (Z/9Z)* = C(5) x C(9) = 4 x 6 = 24.
Il y a donc 24 éléments dans (Z/45Z)*, dont les ordres de ces éléments sont : 1 (pour l'élément 1), 2, 3, 4, 6, 8, 12 et 24.
Dans (Z/5Z)*={1,2,3,4}, les 4 éléments sont d'ordre 1, 2 ou 4.
Dans (Z/9Z)*={1,2,4,5,7,8}, les 6 éléments sont d'ordre 1, 2, 3 ou 6.

Voilà l'allure du treillis finale :

J'ai compris qu'on avait d'un côté les éléments d'ordre 1 2, 4 et 8 (gauche) et d'ordre 3, 6, 12 et 24 (droite).
Mais je n'arrive vraiment pas à voir comment le treillis a été construit... Pourquoi, par exemple, il y a 3 ronds à la ligne "ordre 2" ? ...
Je n'arrive pas à y voir très clair...

[A voir en vidéo sur Futura]

[invite4308cf33]

Je retente le dessin en ajoutant les ordres associés à chaque "ligne".
J'ai entouré en bleu les ronds que je n'arrivais pas à comprendre.

Pourquoi, à l'ordre 2, il y a 3 "ronds" correspondant ?
Pareil pour l'ordre 4, on a le rond correspondant à C4 et celui à C2xC2, mais alors celui du milieu renvoie à quoi ?
Enfin bon, j'ai l'impression d'être plutôt... complètement perdue avec ces treillis (Z/nZ)*

Et par exemple, comment savoir sans calculs laborieux que 2 et 32 sont d'ordre 12 dans (Z/45Z)* ?
Quelle différence entre l'ordre 4 (C4 sur le dessin, je sais qu'il s'agit de groupe cyclique d'ordre 4) et l'ordre C2xC2 (groupe cyclique d'ordre 2 x groupe cyclique d'ordre 2) ?

[Tryss2]

Déjà, C4 et C2XC2 ne sont pas isomorphes : C4 a des élément d'ordre 4 (ses générateurs) tandis que C2xC2 a au mieux des éléments d'ordre 2

Sinon, il y a 3 ronds sous C2xC2, car C2xC2 possède 3 sous groupes d'ordre 2.

C2xC2 = [a,b] (je note comme ça le sous groupe engendré par a et b)

Alors [a] est isomorphe à C2, de même que [b] et que [a+b], et ces trois sous groupes sont différents (je les note additivements)


Pour l'ordre 4, il faut voir que C2xC4 = [c,d], avec c d'ordre 2 et d d'ordre 4

Il y a donc 3 sous groupes d'ordre 4 : [d], [d+c] (isomorphes à C4) et [2d,c] (isomorphe à C2xC2)



Plus généralement : C3xC4xC2 = [a,b,c] ou a est d'ordre 3, b d'ordre 4 et C d'ordre 2, avec a b et c qui commutent, vu que le groupe est abélien

[b,c] est l'unique sous groupe d'ordre 8

Ce sous groupe a 3 sous groupes d'ordre 4 : [b], [b+c] et [2b,c]

Le sous groupe de [b] est [2b], celui de [b+c] est aussi [2b], tandis que [2b,c] a 3 sous groupes : [2b], [c] et [2b+c]