Dans un plan infini, une droite orthogonale ou parallèle?

[blacksages]

PARTIE 1
Bonjour,
j'aimerais faire part d'une réflexion et avoir un avis dessus.
Mes connaissances: maths du collège/lycée, bases en géométrie vectorielle/affine et leur complément en euclidien, plus qlqs connaissances en théorie des courbes.

Définition:
Point de fuite: outil de représentation de l'espace, on associe à une direction de l'espace un point imaginaire où convergent toute droite de cette direction.

Prenons un plan infini PI, nous considérons une partie du plan que nous regardons.
Nous considérons un repère orthonormé du plan.

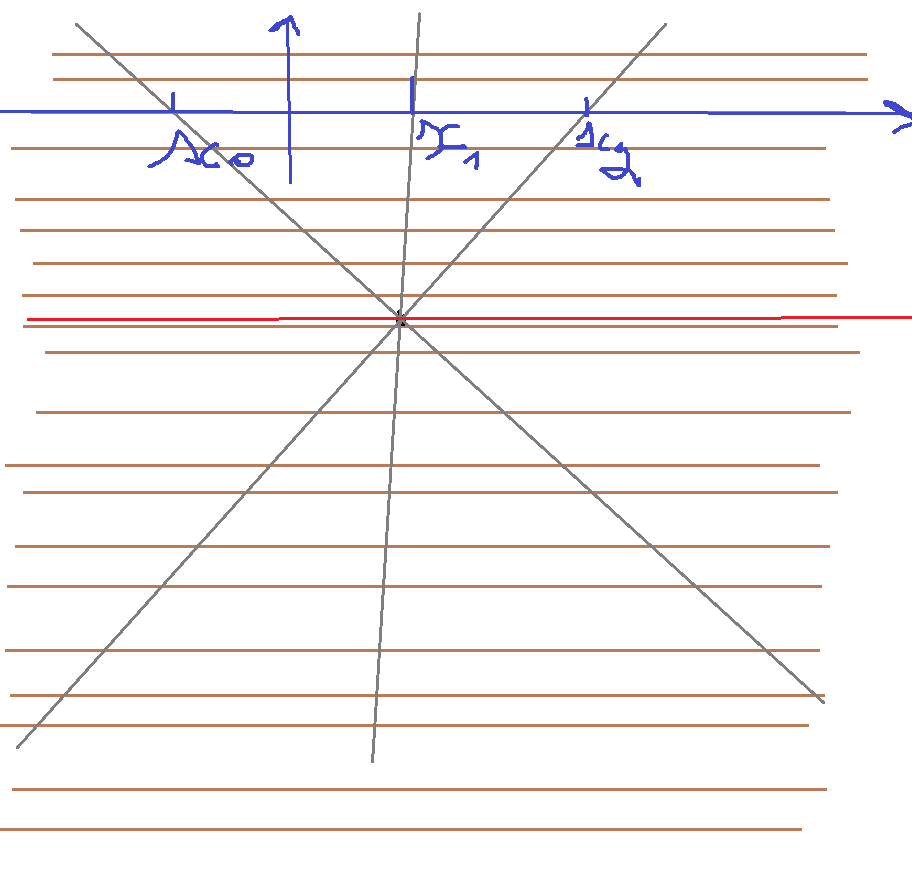
Nous décidons arbitrairement de placer un point de fuite sur ce bout de plan:
(les droites nord-sud convergent toutes vers ce point, les droites ouest-est sont toutes parallèles.)
Notons Xf fixé.
Sans titre0.png

Nous descendons légèrement ce point de fuite, tout en regardant le même bout de plan:
Sans titre1.png
(pas tout à fait verticalement, à la souris c'est pas facile =D)

Nous plaçons ce point de fuite à Yf->-infini
Sans titre2.png
Toujours à Xf fixé.

On note que les droites nord-sud convergent toutes vers un point de fuite infiniment loin de la partie de ce plan.
L'observation démontre que tous les segments du bout de plan sont parallèles, les droites qui les supportent sont donc parallèles.

Prenons le cas dans l'autre sens, nous fixons Xf et Yf, nous considérons une droite d'équation y=Xp+X0p:
1Sans titre0.png
Le point de fuite étant toujours fixé, on considère la droite d'équation y=Xp1+X0p1, avec Xp1>Xp:
1Sans titre1.png
-----

[blacksages]

PARTIE 2

Vous l'aurez compris, nous allons considérer une nouvelle droite d'équation y=Xp2+X0p2 avec Xp2>>Xp, tel que Xp2->+infini:


L'observation démontre que cette droite est parallèle aux droites ouest-est.

Ma réflexion est la suivante.
Quid d'une droite semblable d'équation y=Xp2+X0p2, tel que Xp2->+infini considérant un point de fuite de coordonnée (Xf; Yf), avec Yf->-infini.

A-t-on une telle droite perpendiculaire aux droites nord-sud, ou parallèles à celles-ci? Ou serait-elle diagonale? Vos impressions, mes erreurs?

Merci de votre temps.

[Dlzlogic]

Bonjour,
Votre question n'est pas inintéressante du tout. J'ai été confronté à ce type de problème dans 2 cas :
1- le redressement de façade. Une façade est un plan (hypothèse de travail). On en prend une photo avec un appareil parfait, c'est à dire qu'il n'y a pas de déformation autre que l'effet de perspective.
2- le dessin en 3D. Dans ce cas on parle plutôt de point d'observation (l'oeil de l'observateur) et de point visé. On admet que les notions de verticale et d'horizontal existent.

Ces deux problèmes se résolvent en géométrie euclidienne, à base de Thalès, et non pas avec la géométrie analytique. La géométrie analytique suppose un repère cartésien, dans ce type de repère la notion "tend vers l'infini" est parfaitement précise, mais la notion "=oo" n'existe pas. Il existe la géométrie projective pour résoudre ce type de problème, et c'est elle qu'on utilise en matière de calcul de photos aérienne.

Je tiens à préciser que dans ces deux cas (comme dans d'autres) il est assez rare d'utiliser l'équation d'une droite "Y=aX + b" dans les calculs sauf naturellement sur la papier. On donne à la machine le calcul à faire, et non des équations de droite. Mais ceci est un peu hors-sujet.

[blacksages]

Merci pour votre réponse.

Ces deux problèmes se résolvent en géométrie euclidienne, à base de Thalès, et non pas avec la géométrie analytique.

Mais je ne sais comment écrire la proposition à vérifier ou démentir?
"Dans le plan, à toute droite d et un point O fixé n'appartenant pas à cette droite, pour tout point P de cette droite, la projection orthogonale du vecteur OP sur la droite n'est pas multiple de ce même vecteur"??

Je pense résoudre ça par récurrence et il faut prouver que la projection et le vecteur sont lin indép, déjà je ne sais pas comment prouver ça, et imaginons que j'arrive à résoudre ça par récurrence, mon intuition math me dit que j'arriverai PAS au cas que je pensais, j'ai plutôt l'impression que le cas "à l'infini" ne donne jamais de vecteur projeté multiple du vecteur-même.

Du coup ma question n'aurait plus d'intérêt, mais pourtant, je ne peux m'empêcher de me dire qu'à l'infini j'ai bien un multiple (donc cette idée de parallélisme), comment résoudre ce conflit entre l'observation et le résultat? L'observation est-elle véritablement fausse? (j'ia supposé la prop vraie, mais bon...)

[A voir en vidéo sur Futura]

[Schrodies-cat]

Il y a un problème d’ambiguïté, il faut énoncer les choses en distinguant les droites de l'espace que vous représenter et leur représentation dans le plan de l'image. Par exemple:

On note que les droites nord-sud convergent toutes vers un point de fuite infiniment loin de la partie de ce plan.

Les droites nord-sud sont parallèles et ne se coupent pas, ce sont leurs représentations qui sont concourantes.
Cette question réglée, les choses pourraient être plus claires.

[Schrodies-cat]

Interprétons le dessin de votre post #2 du point de vue de la représentation en perspective, votre point de départ, ou de la photographie:
Vous êtes situé au dessus du plan ou se trouve le plan que vous représentez.
Sous cette hypothèse, les demi droites concourantes situées en dessous de la droite rouge correspondront aux parties des droites nord sud que vous voyez devant vous.
Les demi droites concourantes situées au dessus de la droite rouge correspondront aux parties des droites nord-sud situées derrière vous, elles ne seront pas sur ma photo et n'auront pas à être sur le dessin.
Et la droite rouge correspondra à l'horizon, qu'on peut considérer comme une droite à l'infini du point de vue de la géométrie projective.

[blacksages]

Est-ce le genre de photo que vous avez en tête?


L'image du point de fuite était simplement pour faciliter la transition géométrique, pour mieux comprendre ce à quoi je pensais.
Je n'ai aucune image en tête précisément.

Si la photo en attaché concerne bien ce à quoi vous penser,
concernant les demi-droites au dessus de la rouge, elles sont celles qui se prolongent au-delà du point de fuite, mais elles ne suivent aucun élément physique. (dans le cas de la photo de route, prolonger au delà du point de fuite n'a pas d'intérêt pour la représentation puisque rien n'y est tenu/lié)

Alors si on veut mettre la relation avec une photo, l'horizon n'est-il pas naturellement ouest-est (en ignorant l'effet de courbure de la terre imperceptible)? ne fait-elle pas partie des droites "qui ne subissent aucune déformation de projection"?

Mais si on veut vraiment s'attacher à cette hypothèse de représentation photo/image, il faut ignorer toute continuité de demi-droite au delà du point de fuite, du coup mes dessins ne servent à rien haha!
Mais le problème que je voulais exposer n'est pas limité par ça, je répète, le point de fuite n'était qu'une manière de guider l'esprit, mais je pense que ça embrouille finalement!

[PrRou_]

Bonjour
Pouvez-vous reformuler votre question finalement ?

[blacksages]

Bonjour
Pouvez-vous reformuler votre question finalement ?

REFORMULATION DE MA QUESTION

Je pense pouvoir mieux exprimer ce je cherche maintenant^^:

Soit un plan, une droite d et un point O(n'appartenant pas à cette droite) à distance M de d et appartenant tous deux à ce plan. Soit O' la projection orth. de O sur d et P un point de la droite qui n'est pas O'.

-Si j'étire le vecteur OP' à l'infini, peut-on dire que les droites engendrées respectivement par O'P et OP sont parallèles?

-De la même manière, si je fixe P, en étirant OP à l'infini (en éloignant O de plus en plus) peut-on dire que la droite engendrée par OP est perpendiculaire à d? (O est à une distance infiniment grande de la droite d)

Intuitivement j'ai envie de dire que non, mais j'avais fait des dessins plus haut, et en observant un bout de ce plan (où d'ailleurs on voyait la droite d), l'observation m'a poussé à dire que oui.

Et donc, de ces deux questions, que se passerait-il si on effectuait les deux actions: "étirer O'P à l'infini puis éloigner O à l'infini"

[blacksages]

Et donc j'imaginais que la droite OP serait orthogonale à elle-même vis -à-vis de l'ordre des actions, le titre est un peu racoleur j'avoue, mais je ne sais pas comment le modifier...

*** C'est fait ***

[gg0]

Bonjour.

"Si j'étire le vecteur OP' à l'infini, peut-on dire que les droites engendrées respectivement par O'P et OP sont parallèles?" ?? C'est quoi, étirer à l'infini un vecteur ? je suppose qu'il s'agissant de O'P, non ?
En tout cas, tant que P est sur la droite (d), (OP) n'est pas parallèle à (d), puisque ces deux droites ont un point commun sans être confondues.
Ce genre de mélanges est à éviter, d'autant que la géométrie projective est construite depuis bientôt deux siècles pour traiter correctement ces idées floues (points à l'infini = direction de droites, deux droites ont toujours un point commun, ..). En géométrie euclidienne, il n'y a pas d'outil pratique pour traiter cela. En gros, la position limite de la droite (OP) est bien une parallèle à (d) passant par O, mais il n'y a plus de point P. En gros, si on fixe un point M sur OP, à distance fixe de O, ce point va se rapprocher aussi près que l'on veut d'un point de cette parallèle.

Pour ton deuxième cas, si O se projette toujours sur O' (fixé), et que O s'éloigne, la droite (OP) n'est jamais perpendiculaire à (d)? Elle a cependant une droite limite qui est la perpendiculaire à (d) en P.

Cordialement.

NB : Il n'y a jamais de "perpendiculaire à elle-même".

[PrRou_]

Je précise juste que,
dans la géométrie euclidienne, les notions de parallélisme et d'orthogonalité existent mais il n'y a pas de droite à l'infini ;
dans la géométrie projective, la droite à l'infini existe (attention : elle dépend du repère projectif choisi), mais les notions de parallélisme et d'orthogonalité n'y sont plus définies...

Si on disait que la droite à l'infini est parallèle à toutes les droites du plan dans le sens où le point commun se trouve (forcément) à l'infini, alors cela ne résistera pas longtemps au changement de repère projectif... c'est pourquoi, on ne parle pas de parallélisme en géométrie projective (idem pour l'orthogonalité).