Trouver l'équation d'une courbe définie géométriquement

[Gandhi33]

Bonjour à tous,

Une question que je me pose depuis longtemps :

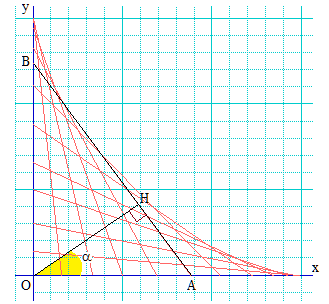
Considérons une barre rigide de longueur 4 dans le premier quadrant du plan. Initialement, les extrémités de la barre sont en (0,0) et (4,0).
On fait glisser la barre de sorte que les extrémités soient toujours sur un axe, pour arriver à la position finale où les extrémités sont en (0,4) et (0,0).
On grise la zone que la barre a traversée (voir pièce jointe).
La frontière entre la zone grisée et la zone blanche est la courbe d'une fonction . Trouver une équation de f.

J'ai essayé sans résultat. La courbe obtenue n'est pas un quart de cercle (ni une fonction de la forme , pour aucun réel ).

Bonne chance à tous si ce problème vous intéresse
-----

[Futonn]

Problème intéressant. La clé du problème est de trouver pour chaque position de la barre le point de la barre qui génère le point de la courbe correspondant...

[Médiat]

Bonjour,

C'est un problème de : Enveloppe d'une famille de droites

[Gandhi33]

Merci beaucoup !

[A voir en vidéo sur Futura]

[JB9197]

Problème de calcul d'une enveloppe de droites.
En généralisant, soit L la longueur de la barre AB (4 dans votre exemple) et soit A l'angle de la perpendiculaire OH à la barre AB


L'équation de la droite AB s'écrit (pente de -OB/OA et valeur de y pour x=0 est OB):
y = -OB/OA*x + OB
y*OA x*OB = OA*OB

On a:
OA= L*sinA
et
OB= L*cosA

d'où l'équation des droites AB en fonction de l'angle a:
y*L*sinA + x*L*cosA = L²*sinA*cosA
ou L n'étant pas nul:
y*sinA + x*cosA = L*sinA*cosA (1)
ou sachant que sin2A = 2*sinA*cosA
y*sinA + x*cosA = L/2*sin2A
soit si L=4
y*sinA + x*cosA = 2*sin2A

On obtient l'équation de la courbe enveloppe en éliminant A du système composé de cette équation des droites en fonction de A et de la dérivée partielle par rapport à A de cette même équation, soit:
y*sinA + x*cosA = L*sinA*cosA (1)
y*cosA - x*sinA = L*cos²A - Lsin²A (2, dérivée partielle de 1)

En multipliant (1) par cosA et (2) par sinA et en soustrayant (1) - (2) on arrive à :
x*cos²A + x*sin²A = L*sinA*cos²A - L*cos²A*sinA - Lsin²a
x = sin²A*sinA (sinus cube de A)
et
y = cos²A*cosA (cosinus cube de A)

En prenant les racines 2/3 de x et y et sachant que sin² + cos² = 1, on a enfin (!) l'équation de notre enveloppe:

x2/3 + y2/3 = L (x et y puissance 2/3).

soit x2/3 + y2/3 = 4 dans votre exemple.

Les tatillons remarqueront que j'ai shunté les pbs de définition aux limites (0,4) et (4,0).

[Gandhi33]

Je n'ai pas encore lu votre message en détails, mais en appliquant la procédure dans Wikipedia, je trouve

y==-(x*(16-(16*x)^(2/3))^(1/2))/((16*x)^(1/3))+(16-(16*x)^(2/3))^(1/2))

soit, en Latex,



je ne sais pas encore si c'est la même réponse que la vôtre.

[Gandhi33]

Je n'ai pas l'impression que les points (0,4) et (4,0) appartiennent à votre courbe alors qu'ils le devraient, non ?

[Gandhi33]

En fait, l'équation que j'avais obtenue est équivalente, après manipulations, à x^(2/3)+y^(2/3)=4^(2/3) !

J'ai lu attentivement ton post, belle manière d'obtenir le résultat . J'ai compris mon incompréhension de tout à l'heure : il y a quelques fautes de frappes dans vos calculs que je me permet de corriger :

"
En multipliant (1) par cosA et (2) par sinA et en soustrayant (1) - (2) on arrive à :
x*cos²A + x*sin²A = L*sinA*cos²A - L*cos²A*sinA + Lsin^3a
x =L sin²A*sinA (sinus cube de A)
et
y =L cos²A*cosA (cosinus cube de A)

En prenant les racines 2/3 de x et y et sachant que sin² + cos² = 1, on a enfin (!) l'équation de notre enveloppe:

x2/3 + y2/3 = L^2/3 (x et y puissance 2/3).

soit x2/3 + y2/3 = 4^2/3 dans votre exemple.
"

Merci pour votre aide et le temps consacré en tout cas

[JB9197]

A la fin j'étais fatigué et j'aurais dû me relire.
Je corrige:

En multipliant (1) par cosA et (2) par sinA et en soustrayant (1) - (2) on arrive à :
x*cos²A + x*sin²A = L*sinA*cos²A - L*cos²A*sinA - Lsin²A*sinA
x = L*sin²A*sinA (sinus cube de A)
et
y = L*cos²A*cosA (cosinus cube de A)

En prenant les racines 2/3 de x et y et sachant que sin² + cos² = 1, on a enfin (!) l'équation de notre enveloppe:

x^2/3 + y^2/3 = L^2/3

soit x^2/3 + y^2/3 = 4^2/3 dans votre exemple.

Ouf!

[JB9197]

Votre correction de mes erreurs a été éditée à 23h56 pendant que je me corrigeais.
On est d'accord, bonne soirée ou bonne nuit.

[Gandhi33]

Effectivement

[RoBeRTo-BeNDeR]

Bonjour, c'est bien ce qu'il me semblait, c'est le quart de la courbe paramétrée "astroïde" définie par x(t)=cos^3(t) et y(t)=sin^3(t).

RoBeRTo