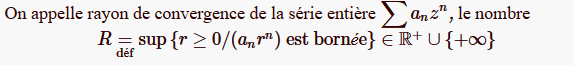Serie entiere Difficulté.

[Nullbytes]

Bonjour,
J'ai un partiel de maths aprés les vacs de noël.. Cela fait 3-4 jours que je bloque sur un annal de l'année dernière. L'annal comporte deux chapitres le premier serie entiere (celui-la → je suis dans la mer**). Aprés Serie de Fourrier, qui me pose nettement moins de difficulté..

Si quelqu'un peut me filer un coup de main cela serai fort sympathique ^^

Capture.PNG

la question ci-dessus je comprends meme pas ce qu'il faut dire... je n'ai aucune idée..


2.PNG

1) Pour calculer R, on fait Alembert ou Cauchy puis 1/l ?
2) F en 0, je remplace dans la serie x = 0 non ?
3) Equadif je suis perdu.
4) On utilise les developpement limité ?

Aprés je pense avoir tout faux je ne comprends pas les series entieres..


Joyeux fetes les gars !
-----

[Tryss2]

La première question est une question de cours... La réponse doit être quelque part dans ton cours. Lis le et apprends le, ça doit être la première des choses à faire

L'idée générale étant que, pour les séries entières, peut inverser la somme infinie et la dérivation. Ou, dit autrement, dériver terme à terme :

si |x|<R,


Pour le deuxième exercice :
1) Attention, tu as un coefficient sur deux de ta série entière qui est nul. Tu ne peux donc pas utiliser le critère de d'Alembert. Ceci dit, on peut toujours revenir à la définition du rayon de convergence (la connais tu?)

2) Oui. Attention ceci dit pour n=0, car tu as du 0^0 (qui vaut 1 dans ce cas bien précis)

3) En dérivant terme à terme, tu as que, quelque soit la série entière f, et pour x à l'intérieur du disque de convergence,



Après, c'est des manipulations sur les sommes, l'idée étant d'écrire ça sous la forme d'une série entière , avec les qui s'écrivent en fonction des

4) Non, c'est juste une manipulation sur les sommes. On fait un changement de variable, en posant X = une fonction de x, et on voit apparaitre une série entière connue en X. Indice :

[Nullbytes]

Merci pour tes réponses !

J'ai une question pour la 1) C'est peut-être débile mais pourquoi une fois sur deux la série est nulle ?
Et pourquoi si la serie est nulle je ne peux pas utiliser Alembert ?
Alembert on peut l'utiliser tout le temps sauf si Un=0 que ce soit négatif ou positif le critère d'Alembert possède des valeurs absolues.
Je ne comprends juste pas cela..
Pour moi, ici on applique d'Alembert en enlevant x^n. Si tu peux juste m'expliquer ce serait top.

Pour la définition du rayon de convergence on l'a vu avec un sup photo ci-dessous :

[Tryss2]

Que vaut le coefficient Un quand n est impair? Dit autrement, par quel nombre est multiplié x^(2k+1) dans ta série?

[A voir en vidéo sur Futura]

[Nullbytes]

Euh.. par (-1)^n non ? Je comprends toujours pas...

Oui, je galère désolé..

[gg0]

écris le début de ta série sous la forme

Par exemple

[Nullbytes]

Je trouve 1 + -x² + (x^(4))/2 + (-x^6)/6 Je ne comprends pas elle n'est pas égale à 0 ? Quelle soit paire ou impaire non ?

[gg0]

Et les x ? et les x^3 ?? Tu en oublies ....

ta phrase est incompréhensible, les "elle" n'ayant pas de mot au féminin à qui se rapporter. C'est d’ailleurs parce que tu restes dans le flou sur les mots que tu ne comprends pas. Tu as lu de travers le message de Tryss2, tu t'es mis une idée en tête que tu n'essaies même pas d'écrire clairement. Tu perds ton temps !

[Nullbytes]

Ok, merci quand même les gars. Avec le stress, Je suis parti en vrille..
Je voulais tout de même savoir vous trouvez combien au rayon de convergence de cette Série ? (Que je sache tout de même).

Merci encore

[Tryss2]

Le rayon est +l'infini. En effet, la série converge pour tout a (et sa somme est facile à reconnaitre)

[Nullbytes]

"Et les x ? et les x^3 ?? Tu en oublies ...."
Sachant que x^2n comment je peux avoir (x,x^3x,...) ça ressemble à du cosinus non ? Ou je suis encore a coté de la plaque ?
Merci

[Tryss2]

Effectivement, tu ne vois pas pas l'éléphant qui est devant tes yeux... rien de grave cependant :

[gg0]

Comme quoi la notion de 0 n'est toujours pas partagée, 10 siècles après son introduction par les mathématiciens indiens

[Nullbytes]

Effectivement, tu ne vois pas pas l'éléphant qui est devant tes yeux... rien de grave cependant :

Ahhh.. Merci !!