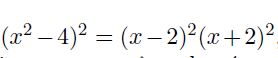je trouve x^4 - 8x^2 + 16
delta est supérieur à 0 donc factorisable, j'ai x^2 - 8x + 16 donne (x-4)^2
si je développe (x-2)^2(x+2)^2 , je retrouve bien x^4 - 8x^2 + 16
mais comment partir de (x^2+4)^2 pour arriver à (x-2)^2(x+2)^2
je sais pas comment faire, pouvez vous m'aider, merci.
Une connaissance classique : x^4 est le carré de x². Donc en remplaçant x par x² dans x^2 - 8x + 16 tu obtiens x^4 - 8x^2 + 16.
Une autre connaissance classique : a²-2ab+b²=(a-b)² Et x^4 - 8x^2 + 16 est justement de cette forme.
Surprenant que tu n'aies pas pensé à une de ces méthodes ...
Cordialement.
NB : Tu es vraiment dans le supérieur ?
identité classique (a²-b²) = (a-b)(a+b)
(x²-2²) = (x-2)(x+2) ==> (x²-4)² = (x-2)²(x+2)²
