Bonjour,
Depuis quelque temps je m'amuse à essayer de trouver un meilleur encadrement du nième nombre premier p(n) que celui actuellement connu qui est :
J'ai un encadrement à proposer quand n est très grand, qui vaut ce qu'il vaut et j'aimerais avoir vos critiques/avis et les erreurs de raisonnement que j'ai pu faire s'il y en a.
J'ai pu remarquer que c'est la borne supérieure de cet encadrement qui pose problème. En effet, alors que la borne inférieure est plutôt près du nième nombre premier, la borne supérieure en est beaucoup plus éloignée.
J'ai donc essayé de rapprocher cette borne supérieure du nième nombre premier, quand n tend vers l'infini.
Il faut donc diminuer la valeur de la borne supérieure, donc soustraire par quelque chose de supérieur à 0.5 mais inférieur à 1 (sinon on tombe sous la borne inférieure).
Il faut également si possible que cette valeur dépende de n pour que ce soit intéressant, sinon on pourrait se contenter de remplacer 0.5 par 0.6 par exemple, ce qui serait peu intéressant car le modèle ne s'adapterait pas suivant n.
Ce que j'ai essayé de faire c'est donc chercher une expression dépendant de n et remplaçant ce 0.5, qui puisse mieux approcher le nième nombre premier depuis la borne supérieure. J'ai pu obtenir quelque chose de valable jusque n=(2.10^17), l'encadrement est meilleur que celui connu. Cependant je ne peux pas tester si c'est le cas quand n tend vers l'infini.
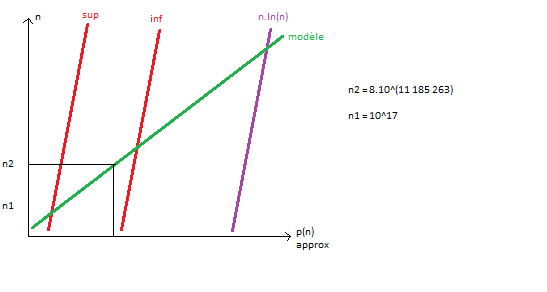
J'ai tracé les droites correspondant aux fonctions n.ln(n) (approximation déjà connue et imprécise), aux bornes supérieures et inférieures de l'encadrement de Dusart et à ma borne supérieure. Sur le graphique j'ai simulé jusque n=10^300 et je vois que ma borne supérieure est bien comprise entre la borne supérieure de l'encadrement de Dusart et la borne inférieure de l'encadrement de Dusart. Cela ne dit pas que le nombre que j'obtiens est bien supérieur au nième nombre premier mais au moins le modèle n'est pas invalidé.
Voici ma borne supérieure avec le nouvel encadrement que je propose :
Bon c'est une borne supérieure assez barbare mais voici mon raisonnement.
Il faut soustraire par quelque chose de supérieur à 0.5 mais inférieur à 1 pour la raison évoquée ci-dessus, il faut donc que cela ne dépasse pas 1 quand n tend vers l'infini. Or on voit avec cette expression que :
Cela va donc dépasser 1 à un moment donné.
Cependant après simulation je m'aperçois que même quand n est gigantesque (de l'ordre de 10^(70 000 000)) cette expression donne 0.85 et des poussières. C'est pour cela que j'ai choisi de composer un grand nombre de fois ln, pour "ralentir" la progression. Et donc ça a l'air de marcher puisque pour n gigantesque on est à 0.85 à peine.
Ce que la théorie dit c'est qu'au bout d'un n on dépassera 1 et le modèle ne sera plus valable. En réalité il ne sera plus valable avant car on passera sous le nième nombre premier, même si on est toujours au-dessus de la borne inférieure de Dusart.
Je fais appel à vous car je ne sais pas si la borne supérieure est toujours au-dessus du nième nombre premier quand n=10^(70 000 000) par exemple. Pour cette valeur de n je sais juste que ma borne supérieure est comprise entre la borne inférieure et supérieure de Dusart. Il faudrait voir si dans le cas général ma borne supérieure est toujours au-dessus du nième nombre premier mais je n'ai aucune idée de comment le démontrer (si c'est vrai déjà).
S'il s'avérait que ma borne supérieure soit au-dessus du nième nombre premier et approche mieux le nième nombre premier que l'encadrement de Dusart, cela serait-il potentiellement intéressant ?
Merci et désolé du long pavé mais j'ai dû expliquer mon raisonnement. Si vous ne comprenez pas quelque chose dites-le-moi.
PS : je précise aussi que mon encadrement ne marche pas pour les petites valeurs de n (par petites valeurs j'entends inférieures à 10^7, j'ai un peu testé le modèle avec quelques grands nombres premiers que je connais et leur n associé).
-----