Bonsoir,
En fait j'ai un problème qui m'a cassé la tête toute la journée :
Je le résumé ici :
Or je suis censé tombé sur la matrice unité car l'application g o g-1 envoie tout couple sur lui même, et la jacobienne de g o g-1 est le produit des jacobiennes de chacune des applications : J(g o g-1) = J(g).J(g-1)
Voilà, si vous pouvez m'aider, ce serait très aimable, merci beaucoup.
-----



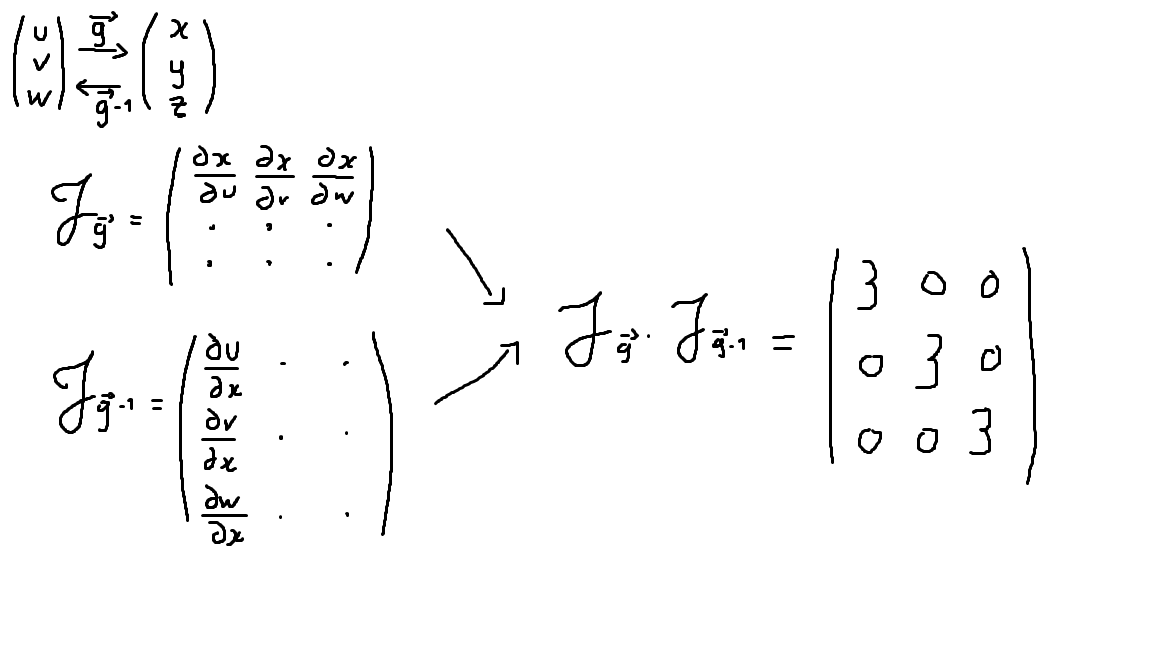

 la jacobienne de la fonction f au point x, alors on a
la jacobienne de la fonction f au point x, alors on a  , on a l'équation matricielle
, on a l'équation matricielle