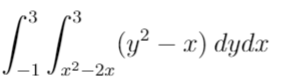Intégrale double et Volume

[ScubaSteve]

Bonjour à tous !
Je suis présentement en train de suivre un cours de calcul à l'université et une notion m'embête un peu.
Nous explorons en ce moment les intégrales doubles définies et le lien qu'elles ont avec le volume d'un solide situé sous la courbe intégré. Cependant , une question de mon devoir me laisse comprendre qu'une intégrale double défine ne représente pas toujours un volume?

La question est la suivante : On me donne cette double intégrale :


Je dois d'abord la calculer (j'obtien une valeur de 768/35 ), mais je dois ensuite spécifié si cette intégrale représente un volume.
Je pense comprendre qu'un volume représente une structure fermé , mais comment puis-je prouver cela? Comment montrer que cette intégrale représente/ne représente pas un volume?

Merci de votre aide !
-----

[gg0]

Bonjour.

Si A est une partie (*) du plan (xOy),

représente, en unités de volumes, le volume (algébrique) de la partie de l'espace située entre le plan (xOy) et la surface d'équation z=f(x,y), pour (x,y) appartenant à A. La question qui t'est posée est de savoir si cette double intégrale (**) peut se ramener à cette forme. Comme je ne connais pas ce que tu as vu en cours, difficile de savoir ce que tu peux écrire.

Cordialement.


(*) Convenable. je n'entre pas dans les détails
(**) cette double intégrale peut être le moyen de calculer une intégrale double.

[ScubaSteve]

Bonjour gg0,
Premièrement, je vous remercie de votre réponse.
Deuxièmement, si j'ai bien compris ce que vous me dites, c'est que si je peux montrer, pour chaque point (x,y) de la région A, que le point associée (x,y,z) sur f(x,y) est au-dessus du plan de coordonné x0y, alors je pourrai affirmer que la double intégrale représente un volume?

Merci

[gg0]

Si tu considères que c'est une question de positivité, oui. Il y a différentes façons de considérer des volumes.

[A voir en vidéo sur Futura]