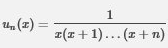décomposition en élèments simples

[kizakoo]

Bonsoir, je bloque sur un exo où l'on demande la décomposition en éléments simples de la fraction :



J'ai essayé de calculer cette décomposition pour n=1 puis essayer de déduire la décomposition pour les autres valeurs de n par récurrence mais je n'aboutis à rien . Pouvez-vous m'aider ?
Merci
-----

[gg0]

Bonjour.

La méthode des pôles simples fonctionne sans problème. On obtient une forme générale, avec des "effets de bord" qui rendent l'écriture générale un peu pénible. Un truc de notation : Une somme de zéro termes vaut 0; un produit de zéro termes vaut 1 (conventions compatibles avec les formules habituelles).

Bon travail !

[kizakoo]

Bonsoir gg0, merci d'avoir répondu … je n'ai pas compris ta réponse. Comment faut-il procéder?

[Resartus]

Bonjour,

on cherche les ak tq : P(x)/[(x-x1)..(x-xk)…] = somme [ak/(x-xk)] dans le cas où les xk sont tous différents (c'est ce qu'on appelle des pôles simples).

L'astuce pour trouver facilement les ak est la suivante :

On multiplie les deux expressions par x-xk. L'égalité reste vraie pour tout x : si on la calcule pour x=xk, à droite il n'y a que ak, et a gauche la valeur pour x=xk de l'expression obtenue en retirant du dénominateur le terme en x-xk. C'est donc le ak cherché

[A voir en vidéo sur Futura]

[gg0]

Pour Kizakoo : ce que vient d'expliquer Resartus est la méthode des pôles simples, qui se trouve au début de tous les cours sur la décomposition en éléments simples. Celui qui a cet exercice à faire est supposé bien connaître la méthode, et l'avoir pratiquée sur des cas plus élémentaires.

Cordialement.

[jacknicklaus]

quand tu auras effectué les calculs indiqués, tu pourras constater que l'on peut arranger le produit sous forme :
1) d'un produit de valeur positives 1,2, ... jusqu'à un certain terme ==> c'est un q! , q à déterminer en fonction de n et k
2) d'un produit de valeurs négatives -1,-2, ... jusqu'à un certain terme ==> c'est un (p!).(-1)^p, p à déterminer.