Représentation de l'inverse multiplicatif

[sleinininono]

Bonjour,

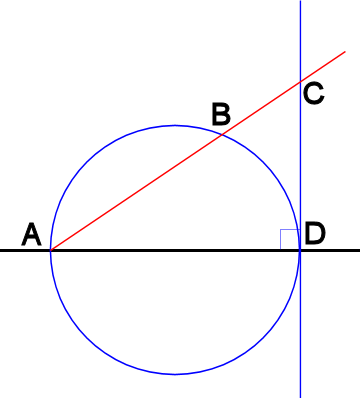
je crois avoir déjà lu une façon de représenter l'inverse multiplicatif avec des cercles... je ne me souviens plus très bien. Avez vous une idée de comment grapher la valeur de l'inverse à partir d'un point ? C'est une méthode qui sert pas seulement dans R mais dans n'importe quel corps.


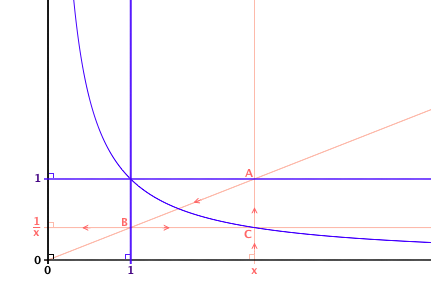
J'essaye de comprendre graphiquement pourquoi la multiplication de l'identité et de l'inverse donne une constante, et peut être que retrouver cette façon d'écrire l'inverse multiplicatif pourrait m'aider.

Je vous remercie d'avance.
-----

[gg0]

Bonjour.

Peux-tu expliquer de quoi tu parles, dans quel cadre tu parles d'inverse, de multiplicatif et de représenter ?

Cordialement

[sleinininono]

Les dessins que j'avais vu étaient dans le cadre de l'arithmétique je crois et de l’algèbre en général, où on prenait un corps particulier et on représenter certaines valeurs, avant de, graphiquement, retrouver son inverse. Je ne sais pas trop quoi dire de plus, c'est des souvenirs vagues.

Après si vous avez une autre interprétation visuelle de pourquoi les fonctions 1/x et x sont des inverses multiplicatifs sur R.

La conclusion à laquelle j'étais arrivée était que les deux fonctions varient de façon identique au cours du temps.
Si une augmente d'une certaine façon vers le bas, alors l'autre fait la même chose vers le haut.

Ce n'est pas le cas pour ln(x) et x, où ln(x) se rapproche plus vite de l'axe Oy (et donc de x = 0 ) que de l'infinie pour y, donc x ln(x) -> 0 en 0.

[ansset]

Après si vous avez une autre interprétation visuelle de pourquoi les fonctions 1/x et x sont des inverses multiplicatifs sur R.

parce que x(1/x)=1 sur R*
pourquoi faudrait il une représentation graphique ?

Ce n'est pas le cas pour ln(x) et x, où ln(x) se rapproche plus vite de l'axe Oy (et donc de x = 0 ) que de l'infinie pour y, donc x ln(x) -> 0 en 0.

drôle d'exemple car ces fonctions ne sont pas "inverse" l'une de l'autre

[A voir en vidéo sur Futura]

[PA5CAL]

Bonjour

Peut-être fais-tu allusion à l'opération géométrique d'inversion, qui permet notamment de représenter la fonction "inverse" f(x)=1/x :



On a la relation AB×AC=AD². Donc en prenant un cercle de diamètre unitaire (AD=1), on a la relation AB=1/AC (ou encore AC=1/AB).

[sleinininono]

oui merci beaucoup c'est exactement cela.

Je ne sais pas si c'est un exemple étrange mais l'idée est là. On comprend souvent la limite de sin x / x en 0 par le fait que sin x ~ x en 0, autrement dit qu'ils ont le même comportement. J'essaye d'étendre cela à d'autres fonctions.

[sleinininono]

j'en profite alors pour demander. Je viens de regarder quelques références à ce propos pour me remémorer les informations.
Il s'avère que pour toute droite passant par l'origine, elle est sa propre inverse. En effet, on voit bien que à part pour 0, tout point est en bijection pour x et 1/x.

Mais avez vous une idée pour faire le passage entre la forme hyperbolique et la droite ? Peut être qu'en passant en 3D on trouve quelque chose ? Je ne sais pas où chercher... Je pensais trouver les réponses avec les ronds de la transformation géométrique inversion mais apparemment ce n'est pas ce dont j'ai besoin.

[gg0]

Sleinininono,

tu es en train de tout mélanger, en confondant inverse et inversion. Et tu ne fais plus des maths, mais de vagues comparaisons sans queue ni tête. Tu as "entendu parler", tu mélanges, tu baratines ... tu perds ton temps. sans parler des incompréhensions genre : "On comprend souvent la limite de sin x / x en 0 par le fait que sin x ~ x en 0, autrement dit qu'ils ont le même comportement" !!!!! Du baratin sur une chose très simple, mathématiquement (*)
Donc inutile que j'essaie de comprendre ce que tu as dans la tête, ça ne concerne pas un forum de maths.


(*) sin(x)~x en 0 est exactement la même chose que limite de sin(x)/x = 1 en 0. Rien à comprendre, c'est une pure traduction de notation.

[PA5CAL]

La question n'est absolument pas claire. J'essaye de lire entre le ligne, mais j'ai du mal à suivre.

La fonction f(x)=1/x peut effectivement être représentée en coordonnées cartésiennes par une hyperbole. Une fois cette hyperbole construite, chaque projection d'un point sur les axes donne des distances à l'origine qui correspondent respectivement à x et 1/x.

On peut donc construire l'hyperbole d'équation y=1/x ou trouver 1/x connaissant x à l'aide d'une construction à la règle et au compas (ou à la règle et à l'équerre) :


[ Faire x --> A --> B --> C et 1/x ]

Si c'est une construction avec des cercles qui t'intéresse, alors il existe un théorème qui dit que toute construction à la règle et au compas peut également être réalisée uniquement au compas. Mais pour ce cas de figure, je ne me suis pas encore penché sur la question...


Est-ce que ça va dans le sens de ce que tu recherches ?