Ensemble et application

invite53514ee9 · 25/10/2018, 01h43

Bonjour,

Je dois faire un exercice sur les ensembles. Cependant, je ne vois pas comment le faire ...
Voici l’énoncé :
Nom : 49FF6E5B-DF1F-4A56-A91F-78C168FE518B.jpeg
Affichages : 273
Taille : 116,2 Ko

Nom : 49FF6E5B-DF1F-4A56-A91F-78C168FE518B.jpeg
Affichages : 273
Taille : 116,2 Ko

Merci d’avance bonne soirée ^^

**minushabens** · 25/10/2018, 08h36

f(X) est un couple donc a priori pas dans P(E). Il y a donc quelque-chose à préciser dans cet énoncé.

**gg0** · 25/10/2018, 08h39

Bonjour.

Tout d'abord, tu dois décoder l'énoncé, comprendre ce qu'est cette application f : quel est l'ensemble de départ, l'ensemble d'arrivée, l'image d'un élément de l'ensemble d'arrivée. Et là tu vas voir un gros problème.
Je te laisse faire ce travail élémentaire (*), reviens avec ce décodage et l'explication de ce qui ne va pas, on verra comment rectifier cet énoncé.

Cordialement.

(*) au sens ou c'est à faire à chaque nouvel exercice.

Edit : Ah ! Minushabens a écrit en même temps que moi et mangé le morceau !

invite53514ee9 · 25/10/2018, 10h38

C’est l’énoncé de l’exercice donc ^^’

Alors, l’ensemble de départ est P(E) et l’ensemble d’arrivée P(E)^2.
L’application associe à x, (XUA,XUB)

A voir en vidéo sur Futura · Aujourd'hui

**gg0** · 25/10/2018, 12h30

Si tu lis bien l'énoncé (" ... f l'application définie sur P(E) à valeurs dans lui-même par ..") Tu vois que l'ensemble d'arrivée est P(E) et que f(X) n'est pas un élément de l'ensemble d'arrivée. Donc l'énoncé que tu as donné au message #1 est incohérent.
On va donc remplacer " l'application définie sur P(E) à valeurs dans lui-même " par l'application définie sur P(E) à valeurs dans P(E)²", comme tu l'as fait spontanément.

Maintenant, décodage de la première question. Que voudrait dire "f est surjective" ? Donc par négation, que veut dire "f n'est pas surjective" ? Bien évidemment, tu écris cela avec des quantificateurs ("quel que soit", "il existe") pour que ce soit facile de nier. Puis "yapuca" ! Si tu fais une représentation en patates, tu devrais voir comment répondre.

Cordialement.

invite53514ee9 · 25/10/2018, 12h40

La définition de surjective :

Screenshot_1.png

La négation est :

Screenshot_2.png

Je dois montrer que la négation est vraie c'est ça ?
Mais je ne vois pas du tout comment m'y prendre ...

invite53514ee9 · 25/10/2018, 12h41

Si j'ai bien compris, je dois montrer qu'il existe un couple qui n'a pas d'antécédent, c'est cela ?

**PlaneteF** · 25/10/2018, 12h51

Bonjour,

Envoyé par Dreamyy

Si j'ai bien compris, je dois montrer qu'il existe un couple qui n'a pas d'antécédent, c'est cela ?

Oui, et c'est pas bien difficile d'exhiber un tel contre-exemple. Un tuyau si tu ne vois pas : Pour un ensemble $\text{[math]}$ non vide quelconque, il y a 2 éléments "remarquables" dans $\text{[math]}$ , qui sont $\text{[math]}$ et $\text{[math]}$

Cordialement

invite53514ee9 · 25/10/2018, 13h08

Donc si on prend le couple (E, ensemblevide), ce dernier n’admet pas d’antécédent donc c’est bon, non ?
Mais je recherche une rédaction rigoureuse. J’ai vraiment du mal dans ce chapitre à rédiger correctement ...

invite53514ee9 · 25/10/2018, 13h09

Merci encore pour toutes vos réponses ❤️

**gg0** · 25/10/2018, 13h20

Dreamyy,

une rédaction rigoureuse est une preuve que $\text{[math]}$ n'a pas d'antécédent, autrement dit que quel que soit X, $\text{[math]}$
Et quand tu vas essayer de la faire, tu vas t'apercevoir que ce n'est pas toujours vrai. Essaie !!

Comme quoi il ne faut pas se jeter sur la moindre indication comme si c'était "La Réponse". En fait, tu manifestes ainsi que tu n'as pas vraiment compris comment fonctionne f. Par exemple f dépend fortement de A et B, que se passe-t-il si A=B ? Ou si A={x} et B={y} où x et y sont des éléments différents de E ? Ou si A et B sont complémentaires dans E ?
C'est ce genre de choses qui permet de bien se rendre comprendre ce qui est donné dans l'énoncé, et de faire le travail.

Bon travail de réflexion personnelle !

invite53514ee9 · 25/10/2018, 13h38

Je dois donc distinguer des cas si j’ai bien compris :

Si A et B sont non-vides, alors le couple (E, ensemble vide) n’a pas de solutions.
Si À et B sont vides, alors on obtient f(X) = (X,X) mais cela n’est pas toujours vrai ?

**gg0** · 25/10/2018, 14h43

"Si A et B sont non-vides, alors le couple (E, ensemble vide) n’a pas de solutions." Justification ? A-t-on besoin de A et B non vides ou on peut demander moins ?
"mais cela n’est pas toujours vrai ? " je ne comprends pas ce que veut dire cette phrase. Exprime-toi clairement, on ne sait pas ce qui est dans ta tête.

Et il te faut toujours rédiger une démonstration ... ça traine !

**PlaneteF** · 25/10/2018, 15h26

Dreamyy,

J'ai l'impression que ceci :

Envoyé par PlaneteF

Un tuyau si tu ne vois pas : Pour un ensemble $\text{[math]}$ non vide quelconque, il y a 2 éléments "remarquables" dans $\text{[math]}$ , qui sont $\text{[math]}$ et $\text{[math]}$

t'a plus embrouillé que véritablement aidé

Garde juste cela en tête, ça peut simplement donner des idées, mais cela ne fait pas l'exercice en soi

Cordialement

invite53514ee9 · 25/10/2018, 18h14

Si f est surjective, (ensemble vide,ensemble vide) a un antécédent C:

AUC = ensemble vide et BUC = ensemble vide, donc A = B = ensemble vide.
Alors pour tout X appartenant P(E), on a f(X) = (X,X) et (E, ensemble vide) n'a pas d'antécédent.

Ainsi (ensemblevide,ensemblevide) ou (E,ensemble vide) n'a pas d'antécédent et f n'est pas surjective

**gg0** · 25/10/2018, 22h03

Ceci n'est pas une démonstration, mais un texte rédigé pour toi, pour t'éclaircir les idées. Reste à rédiger un texte compréhensible par toute personne qui a eu le même cours que toi, si possible organisé.

Bon travail !

invite53514ee9 · 25/10/2018, 22h33

Je dois maintenant montrer que f est injective si et seulement si A inter B = vide.

Je n'arrive pas à faire la réciproque.
J'ai raisonné par double équivalence.
Cependant pour la réciproque :

je suppose qu'on a A inter B.
Je veux montrer que f est injective mais comment m'y prendre ... ? merci

Enfin pour la question 1, est-ce que mon dernier message est juste et je peux écrire ça sur ma copie ?

**gg0** · 25/10/2018, 22h45

Ta dernière question montre que tu n'as pas lu mon dernier message. J'y réponds par avance.

En supposant A inter B = vide, que dois-tu montrer, pour justifier que f est injective (caractérisation de l'injectivité, ou définition) ?

invite53514ee9 · 25/10/2018, 22h50

Il faut prendre 2 éléments de l'ensemble d'arrivée et montrer qu'il possède le même antécédent.
Autrement dit :

Si f est une application qui va de X dans Y alors :

Nom : Screenshot_1.png
Affichages : 140
Taille : 2,4 Ko

Nom : Screenshot_1.png
Affichages : 140
Taille : 2,4 Ko

**gg0** · 26/10/2018, 07h53

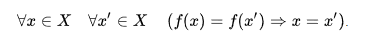
OK.

Donc dans ton exercice, il faut prouver ....

invite53514ee9 · 26/10/2018, 08h14

Soit (XUA, XUB) = (X’UA,X’UB),
Je dois prouver que X = X’

Mais je ne vois pas trop comment m’y prendre

**gg0** · 26/10/2018, 10h10

Il faut utiliser l'hypothèse, en partant de la signification de l'égalité de ces deux couples (tu manques vraiment de volonté de faire de ne pas avoir traduit tout de suite cette égalité.

"je ne vois pas trop comment m’y prendre " Qui n'essaie rien n'obtient rien !

**PlaneteF** · 26/10/2018, 13h23

Bonjour,

Envoyé par Dreamyy

Soit (XUA, XUB) = (X’UA,X’UB),
Je dois prouver que X = X’

Mais je ne vois pas trop comment m’y prendre

Voyons, voyons, ... Il y a a minima la méthode archi classique et standard que tu dois connaître, qui consiste en ceci : Soit $\text{[math]}$ , et tu montres que $\text{[math]}$ . C'est quand même le b.a.-ba des démonstrations sur les ensembles. En plus ici cette démonstration est vraiment très courte et très simple. A noter que vu la symétrie formelle entre $\text{[math]}$ et $\text{[math]}$ , tu peux te contenter de cela

Cordialement

**PlaneteF** · 26/10/2018, 16h34

Envoyé par PlaneteF

Soit $\text{[math]}$ , et tu montres que $\text{[math]}$ . C'est quand même le b.a.-ba des démonstrations sur les ensembles. En plus ici cette démonstration est vraiment très courte et très simple. A noter que vu la symétrie formelle entre $\text{[math]}$ et $\text{[math]}$ , tu peux te contenter de cela

Je précise, dans le cas le plus général tu dois bien sûr démontrer la double inclusion pour démontrer l'égalité de 2 ensembles, mais ici, compte tenu de la symétrie évoquée, une seule inclusion suffit (mettre la justification de la symétrie dans ta rédaction bien évidemment)

Cordialement

**ansset** · 26/10/2018, 16h55

@Planete:
pas sur de saisir ta démo,(*)
de plus, la condition $\text{[math]}$ n'intervient pas !?

(*) pense même pouvoir proposer un contre-exemple , présentée tel qu'elle.

**ansset** · 26/10/2018, 17h04

je trouvais l'explication de l'autre post plus claire.
à condition déjà de justifier l'implication préalable sur l'égalité des intersections , puis de développer cette formulation.

**PlaneteF** · 26/10/2018, 19h32

Envoyé par ansset

@Planete:
pas sur de saisir ta démo

Quelle démo ? Je n'ai présenté aucune démonstration en particulier, je rappelle juste à Dreamyy la façon standard de démontrer l'égalité de 2 ensembles, ... chose qu'il souhaite faire

Et si, pour démontrer une inclusion tu es bel et bien obligé d'utiliser $\text{[math]}$

Cordialement

invite53514ee9 · 26/10/2018, 20h10

Merci à vous tous pour vos réponses. J'ai cherché un peu et j'ai trouvé merci encore et à très bientôt. Bonne continuation !

Ensemble et application