Démonstration Surface de révolution

[mAx6010]

Hello,
Je mets ce thread dans cette section, même s il pourrait être dans la section math college/lycée ou Physique.
Je recherche une démonstration mathématique de la compensation d un effort radial sur une géométrie de révolution.
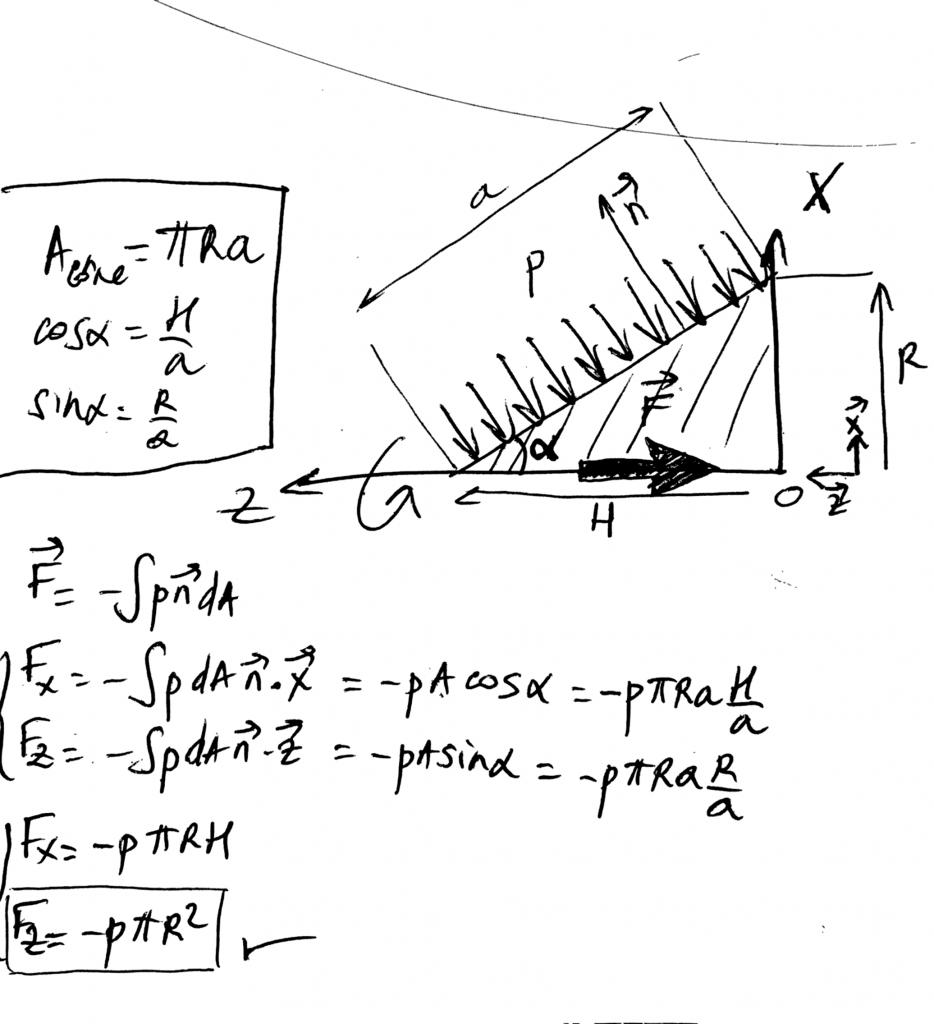
Je prends un exemple simple: la résultante des forces de pression sur un cône de Rayon R (suivant l axe x)et de hauteur H (suivant l axe z) (je ne prends pas en compte la base du cône).
Je peux démontrer que la force est dirigée suivant l axe de révolution (axe z), et ce en me limitant dans un le plan (xz). (cas académique vu et revus pendant ma scolarité)
Je décompose donc ma force résultante sur les 2 axes du plan, et j élimine la composante radiale (vecteur x) car elle est compensée par "révolution"
Et c est justement cela que j aimerai démontrer mathématiquement. (en gros la somme des vecteurs x par rotation autour de l axe z)

ça doit être tout bête, mais je suis énormément rouillé
Merci par avance
Maxime
-----

[ansset]

Un dessin serait plus clair !
On ne sait ou se situent tes axes , ni le point d'application de ta force.

[mAx6010]

Je mets un croquis des que je rentre.
La force est calculée en intégrant la pression (constante) sur toute la surface du cône tout simplement.
Évidemment le champ de pression est normal à la surface du cône

[gg0]

La résultante des forces de pression sur deux éléments infinitésimaux de surface symétriques par rapport à l'axe est dirigée suivant l'axe.

Cordialement.

[A voir en vidéo sur Futura]

[Dynamix]

Salut

Évidemment le champ de pression est normal à la surface du cône

La pression est une grandeur scalaire , elle ne peut pas être normale à quelque chose .
Ce que tu cherches découle du théorème du gradient .
https://fr.wikipedia.org/wiki/Th%C3%...me_du_gradient

[mAx6010]

Le croquis en question fait à la va-vite.
Mon champ de pression est un champ de vecteurs

[Dynamix]

Mon champ de pression est un champ de vecteurs

Re NON !
Les flèches représentent des forces (de pression) , pas des pressions .

Tes intégrales sont incomplètes : tu ne précises pas sur quoi tu intégrés.
Si c' est sur le cône , Fx est nul .

[mAx6010]

Re NON !
Les flèches représentent des forces (de pression) , pas des pressions .

Ok si tu veux. Je m incline

Tes intégrales sont incomplètes : tu ne précises pas sur quoi tu intégrés.
Si c' est sur le cône , Fx est nul .

OUi je me mélange les pinceaux.
Si mon Fx est non nul , alors mon Fz ne peut pas être la résultante finale
D ou ma demande sur le forum.
Et oui c est exactement ce que je demande: comment démontrer que Fx est nul (en intégrant sur tout le cône).

La somme de mes vecteurs x (par révolution) doit être nulle; mais j vois pas comment le faire apparaitre mathématiquement.
De la même manière la somme des vecteur z (par révolution) doit me donner le résultat Fz.

[Dynamix]

Et oui c est exactement ce que je demande: comment démontrer que Fx est nul (en intégrant sur tout le cône).

Si la surface est fermée , la résultante est nulle vu que le gradient de pression est nul .
Si la surface est ouverte , la résultante n' est pas nulle .
Si tu décomposes la surface fermée en tronc de cône (S1) et disque (S2) tu as :
F_(S1) + F_(S2) = 0

[mAx6010]

La surface est ouverte, c'est bien S1.
Et oui la résultante n est pas nulle, puisque elle est égale à mon Fz précédemment calculé.
Ce que je veux c est démontrer que la composante radiale s annule par révolution.
Après effectivement comme tu le soulignes, Si je décompose sur la surface fermée alors mon "corps" est en équilibre et alors nécessairement F(S1) + F(S2) = 0
D’où F(S1) = F(S2) = Fz =p* S2 (au signe près) avec S2=pi*R^2
Mais ce n est pas cette démarche que je recherche

[gg0]

Bonjour.

Tu traites le cas où le champ de pressions est constant. Tu sembles avoir oublié qu'il s'agit d'une surface de révolution, donc qu'il y a un côté opposé. Et même tout un cône ! Donc intégrer sur un segment est absurde !! Il faut intégrer sur tout le cône. Avec des intégrales de surface.

Cordialement.

[mAx6010]

J ai integré sur la surface entière:
Je ne parle pas de la composante Fx, car le calcule est faux (je le sais et c est le but de ce thread)

Pour la composante Fz le calcul est bon, avec intégration sur toute la surface (ouverte).

Je cherche une démonstration rigoureuse de :

avec vecteur unitaire radial

On peut le retrouver avec la méthode de Dynamix (excellente d'ailleurs), mais le résultat est déduit de l équation d’équilibre sur la surface du cône fermée et non purement calculée .

[gg0]

Désolé,

je ne sais pas ce que tu calcules, et ton schéma est celui d'un triangle, pas d'un cône. Si tu intègres vraiment sur la surface du cône, le vecteur normal aura des composantes en y généralement non nulles. Il faut donc traiter correctement cela (3 dimensions, pas 2).

Et tout ça pour rien, car il y a une symétrie par rapport à l'axe Z qui annule l'intégrale sur toute direction perpendiculaire à l'axe Z (intégrale d'une fonction impaire).

Cordialement.

[mAx6010]

Sur mon schéma l axe z est l axe de révolution (j y ai bien mis un symbole de rotation autour de l axe).
On peut aisément imaginer le cône (de révolution).
Si l axe des y vous gêne (je peux comprendre) remplacez-le par un axe dont le vecteur unitaire (ur) est un vecteur unitaire perpendiculaire à l axe de rotation de vecteur unitaire (uz) et indépendant de l angle de rotation (ce que j appelle radial). Les forces de pression seront toujours dans le plan (uz;ur)
Après je pense qu il faut passer par un autre repère type cylindrique

[Dynamix]

Et tout ça pour rien, car il y a une symétrie par rapport à l'axe Z qui annule l'intégrale sur toute direction perpendiculaire à l'axe Z (intégrale d'une fonction impaire).

Même sans symétrie , vu que le résultat ne dépend pas de la surface .
Il dépend uniquement de l' ouverture (la courbe qui limite la surface)

[mAx6010]

Mais la question etait justement de le demontrer sans utiliser la/les symetrie(s)
J en conclue que ce n est pas aussi evident que cela.
Mais je me contente de la deduction proposee par Dynamix au post #9