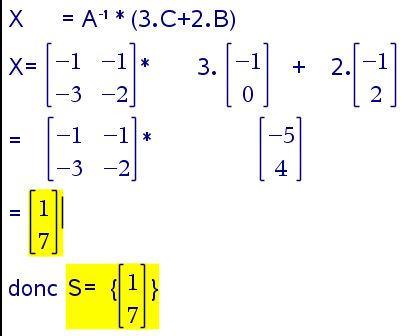déduire la solution de l'équation

[invite660d5fc4]

	Bonjour J'ai un exercice de maths et je ne sais pas par où commencé , après avoir calculer l'inverse de la matrice A : a.JPG voici l'énoncé de l'exercice de mes soucis:
	je dois en déduire la solution de l'équation: AX-2.B= 3.C tt.JPG ma proposition que j'ai mis c'est d'abord j'ai déterminé les équations de matrices , puis j'ai essayer de développer par rapport au comatrice de transposé de la valeur A ci dessus: ttd.JPG aaz.JPG mais le soucis je suis bloqué pendant des heures sur l’équation car j’hésite pour savoir si je dois multiplier par 3* la comatrice de transposant de C et 2* la comatrice de transposant de B ou bien mes raisonnements sont totalement faux .............. Pourriez vous m'aider s'il vous plait Je vous remercie d'avance

-----

[gg0]

Bonjour.

En attendant de pouvoir lire tes documents, je te rappelle que tu as simplement à résoudre AX=2B+3C, ce qui se fait comme d'habitude (j'espère que A est inversible), puisque 2B+3C est une matrice.

Cordialement.

[invite660d5fc4]

Bonjour,

oui je sais, pour déduire la solution de l’équation que j'ai fais pour résoudre: AX-2.B= 3.C

c'est j'ai d'abord déterminer les matrices de mon équation:
or AX -2.B= 3.C
AX -2.B+2.B= 3.C+2.B
AX = 3.C+2.B
A^-1 AX = A^-1 (3.C+2.B)
I^2 X = A^-1 (3.C+2.B)
X = A^-1 * (3.C+2.B)

donc
X = 3. A^-1 * C + 2.A^-1 * B
j'ai fais 3* la comatrice de transposé *C + 2* la comatrice de transposé * B et je ne sais pas quels valeurs prendre pour calculer

donc X= 3. [-1,-1] * [-1] + 2. [-1, -1] * [-1]
[-3,-2] [0] [-3, -2] [2]
= 3. [1] + 2. [-1]
[3] [-1]
= [1]
[7]
donc S = [1]
[7]


PS: désolé si c'est mal rédiger ma matrice,

[gg0]

Bonjour.


Ton résultat est évidemment faux, X ne peut être qu'une matrice 2x1, un vecteur colonne.
Et tu te compliques la vie inutilement. 3C + 2B est un vecteur colonne très simple, le multiplier par A^-1 que tu as calculé (c'est ce que tu dis) est fait en 20 secondes. pas besoin de parler de comatrice, tu fais la multiplication de la matrice carrée 2x2 A^-1 par le vecteur 2x1 V=3C+2B.

Bon travail !

NB : Si tu veux d'autres explications, commence par donner l'expression de la matrice A^-1 et celle du vecteur 3C+2B

[A voir en vidéo sur Futura]

[invite660d5fc4]

voici les expressions du vecteur 3.C+2.B sur l'image ci dessus:


l'expression de la matrice A^{-1} c'est : X= A^ {-1}* (3.C+2.B)

[gg0]

OK,

sauf la dernière ligne où tu racontes n'importe quoi. Mais peut-être ne comprends-tu pas ce que veut dire "l'expression de la matrice". Il s'agit de dire simplement comment elle s'écrit.

[invite660d5fc4]

Bonjour
voici l'expression de la matrice que j'ai écris ci dessus:

[invite51d17075]

elle l'était déjà dans la dernière pièce jointe de ton premier post, mais sans la nommer comme la matrice inverse.
c'est donc surtout une question de présentation dans la résolution.
ps : pas encore vu ta pièce jointe.

[gg0]

Lozagri,

j'ai expliqué ce que signifie le groupe de mots "l'expression de la matrice A^{-1}". Tu sembles ne pas vouloir comprendre. Et ne même pas comprendre que si tu écris "X = ..." tu parles de X, pas de A^-1.
Inutile de demander des commentaires sur ton travail si tu ne lis pas les réponses.