Solutions a l'équation exp(x)-exp(i*x)=x

[extrazlove]

Bonjour à tous et à rien,

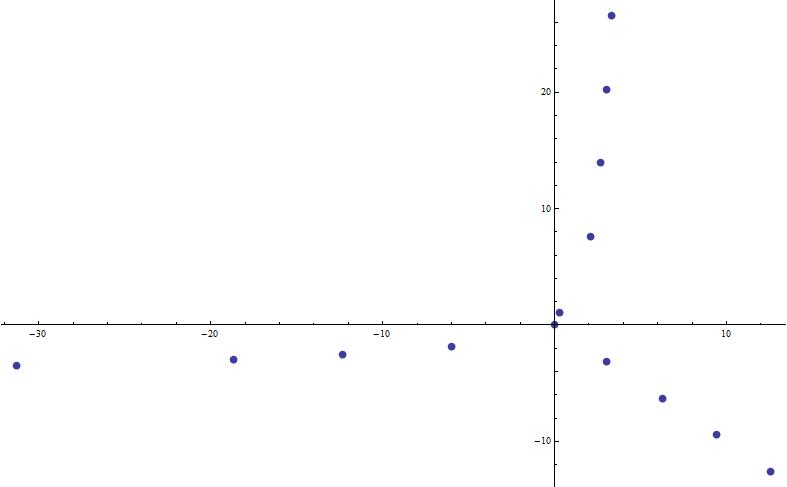
Je cherche a Déterminer une solution autre que x=0 pour l’équation exp(x)-exp(i*x) )=x dans le plan complexe


Quand x tend vers 0 je peux faire le développement limité de exponentiel .

exp( x)=1+x/1!+x^2 /2!+x^3/3!++x^4 /4!-x^5 /5!.... et exp (i*x)=(1+(i*x)/1!+(i*x)^2 /2!+(i*x)^3 /3!+(i*x)^4 /4!-(i*x)^5 /5!....


Donc exp x- exp i*x=1+x/1!+x^2 /2!+x^3/3!+.... -(1-(i*x)/1!+(i*x)^2 /2!+(i*x)^3 /3!+(i*x)^4 /4!-(i*x)^5 /5!....
=(1-i)*x/1!+(1-i)(x^3/3!)+(1-i)*(x^5/5!).....
=(1-i)(x/1!+x^3 /3!+(x^5/5!)....
=x

Donc je peux conclure que la partie imaginaire est nul donc x/1!+x^3 /3!+x^5/5!.....=0 et que x/1!+x^3 /3!+(x^5/5!)....=x avec x#0 car x est juste au voisinage de 0 et je peux dire que (1+x^2/3!+x^4/5!+...)=0 donc que x^2/3!+x^4/5!+...=x(x/3!+x^3/5!....)=-1

donc 1/x=-(x/3!+x^3/5!....) quand x tend vers 0 donc 1/x tend vers l'infini donc je peux dire que -(x/3!+x^3/5!....) =x^n/(n+2)! grace au développement limité aux voisinage de l'infini.
donc 1/x=-x^n/(n+2)!
donc x^n+1=-(n+2)!
donc exp((n+1)log(x))=(n+2)!

(n+1)log(x)=log(-(n+2)!)
log(x)=log(-(n+2)!) /n+1

x=exp(log(-(n+2)!) /n+1)
=(exp(log(-(n+2)!) )^(n+1)
=(-(n+2)!)^(n+1)

est une solution a exp(x)-exp(i*x) )=x quand n tend vers l'infini.

Est ce que mon raisonnement est logique est x=(-(n+2)!)^(n+1) quand n tend vers l'infini est une solution a cette équation?
-----

[albanxiii]

Bonjour,

Votre équation s'écrit exp(x) - x = exp(ix), soit en séparant les parties réelles et imaginaires : exp(x) - x - cos(x) = 0 et sin(x) = 0.
A partir de là, c'est résolu.

[eudea-panjclinne]

Est ce que mon raisonnement est logique

Malheureusement, tes calculs sont fantaisistes.
Tu mélanges des sommes finies avec des sommes infinies de séries, ce qui ne peut se faire que sous des conditions précises.
Tu fais tendre x vers 0 et le n du terme général des séries vers l'infini ce qui dans tes calculs n'a aucun sens, comme ta phrases :
est une solution a exp(x)-exp(i*x) )=x quand n tend vers l'infini.

Considère et étudie ce que t'a dit @albanxiii.

[Resartus]

Bonjour,
Euh, si on considère que x peut être complexe, pas tout à fait d'accord avec albanxiii, car les parties réelles et imaginaires de exp(ix) ne sont pas cos(x) et sin(x)

Numériquement, Wolfram ne fournit qu'une racine non nulle https://www.wolframalpha.com/input/?...xes&wal=header

Mais il y en a une infinité, qui se rapprochent de n(1-i)pi quand n tend vers l'infini
On peut le vérifier en écrivant l'équation sous la forme 1-exp((i-1))x)=x/exp(x)

Quand x devient très grand, la partie de droite tend vers zero, et donc celle de gauche aussi...
Ce qui donne x proche de 2i.n.pi/(1-i)= (1-i).n.pi

[A voir en vidéo sur Futura]

[gg0]

Voir aussi sur cet autre forum un joli dessin. Qui explique l'existence d'une infinité de solutions.

Attention, Resartus, c'est quand la partie réelle de x tend vers l'infini, il n'y a pas de n dans l'énoncé de la question.

Cordialement.

[JB2017]

Bonjour
Dans \C l'ensemble des solutions est discret, non borné mais on peut (on doit pouvoir) analyser le comportement asymptotique.
Ci dessous les solutions calculées dans un rectangle qui contient 0.

[gg0]

Les solutions de Resartus sont celles qui sont dans le quatrième quadrant, et il en donne des approximations obtenues en prenant n grand.

Cordialement.

[JB2017]

Les solutions de Resartus sont celles qui sont dans le quatrième quadrant, et il en donne des approximations obtenues en prenant n grand.

Cordialement.

Bonjour
Je ne comprends ta remarque qui semble dire qu'il n'y a qu'une seule branche asymptotique.
Alors que déjà mon calcul numérique montre qu'il semble y en avoir 3..
Je ne vais faire une analyse complète mais par exemple
mais je peux prouver qu'il existe des solutions, disons z_k=log(pi/2+k pi)+ i (pi/2+k pi) +o(1) lorsque k\in N tend vers l'infini
Par exemple avec k=300 on trouve numériquement z_k\approx 6.85018+ 944.049 i
Il est surement possible d'améliorer le o(1) mais c'est assez technique et j'ai pas regardé pour cette équation.



J'ai pas trop lu en détail le message de Resartus mais vite fait il ne donne qu'une branche, peut être celle la plus facile à trouver le comportement asymptotique .

[gg0]

Non, non, je ne dis pas qu'il y a une seule branche. On voit bien sur ton schéma les trois branches, et même l'aspect exponentiel de celle que tu cites. Je me suis contenté de rapprocher ce qu'il dit de ton schéma.
Mais manifestement, son explication est un peu fautive, il manque deux autres séries de solutions.

Cordialement.

[Resartus]

Bonsoir,
Groooosses bêtises en effet de ma part....

JB, pourrais-tu nous dire quel logiciel tu as utilisé pour trouver les zéros?

[JB2017]

Bonjour
Il faut que je sois honnête. Ici j'ai fait le calcul numérique, ce qui m'aide à voir les branches possibles et seulement ensuite
je fais (je devrais faire une vraie analyse pour confirmer le calcul numérique) et si possible on calcule le comportement asymptotique des racines.

Concernant le logiciel c'est n'importe lequel. Le programme je l'ai fait moi même, le dessin est fait avec mathematica.

C'est un programme que j'ai ressorti où j'avais dû illustrer numériquement des résultats de calculs des valeurs propres de certains opérateurs qui avaient une résolvante compacte. En gros j'avais les résultats théoriques, je savais où était les valeurs propres et le calcul numérique était une sorte de confirmation des calculs.

Ici on a l'équation brute, on ne sait pas d'où elle vient, mais le dessin montre un peu ce qu'il se passe. Pour une des 3 branches infinies j'ai fait un début de comportement asymptotique (celui que j'ai donné) mais la suite semble un peu plus compliqué à cause du logarithme. Autant dire, qu'on a le Dl des "zk" jusqu'au o(1) assez facilement, ensuite pour être plus précis, il faut se fatiguer.