Trigonométrie
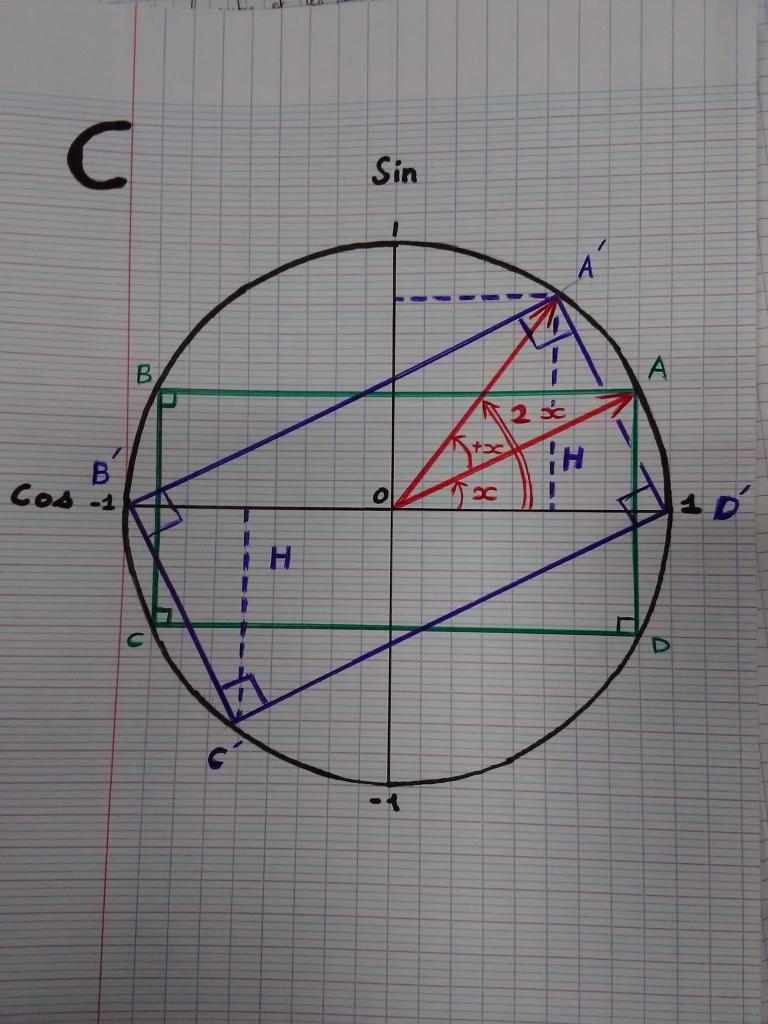
Salut à tous !
Une petite question à laquelle je dois répondre me pose problème, on me dit "Sachant que 0<x<pi/2 et que sin(x) =sin(2x) que vaut x ?
Alors voilà je me dis que x se trouve sur le premier quadrant. Si sinus(x) =sin(2x) alors j'en ai déduis que le sinus devrait être égal à 0. Or cela serait impossible vu que x est strictement entre 0 et pi/2.
S'il-vous-plaît, quelqu'un pourrait m'aider ? 😊
Bonjour. Où est la physique?
On a. L'équation est donc
On peut diviser des deux côtés par
On a donc
Mais on peut s'épargner cet effort de mémoire et ces calculs en faisant un petit dessin, un cercle trigonométrique avec un triangle dedans.
Oups pardon je suis un peu tête en l'air j'aurais dû le mettre dans la discussion math
Et merci beaucoup à vous pour votre réponse ! En essayant de faire le cercle trigonométrique je trouve en effet pi/3 (bien plus rapide effectivement) mais je ne vois toujours pas ce que viens faire le sin(2x) dans tout ça étant donné que j'ai trouvé pi/3 sans cela
Bonjour,
Non, c'est la solution de l'équation sin x = sin 2x. Sans équation, on a pas de solution. sin (pi/3) étant égal à sin(2pi/3). Et oui toujours transcrire les équations en géométrique, c'est tout de suite plus simple! On ne peut pas trouver pi/3, si on a pas sinx = sin(2x). On part bien de sin(2x)=2cosx sinx. Après pourquoi sin(2x)=2 cosx sinx? Mystère!
Ah ouii j'étais un peu distraite j'avais fait le bon raisonnement de base mais j'ai melangé quelques éléments au moment d'avoir écrit la réponse ! Merci d'avoir pris le temps de me répondre
Bonjour,
J'ai déplacé la discussion en maths.
Envoyé par jeanbon22
Non, ça n'est pas un mystère, c'est de la trigonométrie.
Cela fait plusieurs messages dans lesquels vous écrivez des choses soit fausses, soit "même pas fausses", mais en tout cas sans rapport avec le sujet et qui ne peuvent que semer la doute dans l'esprit des poseurs de question.
Je vous demande de vous arrêter (c). Ne postez plus sur ce que vous ne connaissez pas.
Not only is it not right, it's not even wrong!
Bonjour,
Oui, pardon. Ca manque de rigueur en effet. Et il n'y a pas de grand mystère derrière. Je te présenterai une démonstration évidente. Pas de calcul, pas de chaine logique, c'est une évidence vu d'un point de vue purement géométrique. Le seul littéral à connaître, c'est le calcul de l'aire d'un rectangle et d'un triangle, après ça saute au yeux. Tu peux voir par toi même.
Tu dessines un rectangle quelconque inscrit dans le cercle avec pour centre le centre du cercle, où la largeur et la longueur sont respectivement parallèle aux abscisses (cosinus) et aux ordonnées (sinus). Tu nommes un coin du rectangle (celui à droite, en haut) x. Tu traces le points 2x sur le cercles, et tu traces le triangle inscrit avec le diamètre du cercle trigonométrique comme base, et le triangle opposé. Tu constateras que le rectangle ainsi formé, est le même que le précédent.
Tu viens d'effectuer une rotation du rectangle, comme tu fais une rotation de x, le point de côté opposé à x, va se trouver exactement sur l'axe cosinus (l'abscisse), ce qui démontre que les deux rectangles ainsi tracés, ont un côté égal, étant inscrit, ils sont forcément égaux.
L'aire du premier rectangle est égale à 2cox par 2sinx. Et le second aussi étant le même. Le second est constitué de deux triangles. Dont la hauteur est sin 2x. La base du triangle est égale à 2. Donc l'aire du triangle est égale à 2 fois sin 2x divisé par 2. Et du rectangle complet 2 sin 2x.
On obtient ainsi 2 sinx fois 2 sinx = 2 sin 2x, et ce qui nous donne sin 2x = 2 cos x fois sin x.
Si tu le souhaites, je peux réaliser les dessins. Ca n'a rien de bien extraordinaire.
Erratum
On obtient ainsi 2 sinx fois 2 cos x = 2 sin 2x, ....On obtient ainsi 2 sinx fois 2 sinx = 2 sin 2x, et ce qui nous donne sin 2x = 2 cos x fois sin x.
Un petit schéma vaut mieux qu'on long discours.
Dans votre message #7 je relève des confusions entre point et coordonnées, qui font que le message n'est pas clair du tout. J'ai perdu le fil à partir de "Tu traces le point 2x sur le cercle" (pas besoin de pluriel, au passage) : je ne comprends pas ce que vous voulez dire. Si on appelle x l'abscisse, comme c'est la tradition quand on ne défini pas ses notations, le point d'abscisse 2x n'est plus sur le cercle.
Du coup, je ne peux pas dire si la suite est correcte ou non, puisque je ne peux pas aller plus loin.
Not only is it not right, it's not even wrong!
Bonjour.
La formule sin(2x)=2 sin(x) cos(x) est une conséquence immédiate de la formule d'addition
sin(x+y) = sin(x) cos(y) + sin(y) cos(x)
où on prend y=x.
Cette formule d'addition a des preuves simples, comme par exemple celle qui est sur ce document.
Une preuve bien rédigée vaut mieux qu'un long discours confus.
Cordialement.
NB : Une preuve basée sur les définitions strictes de sin et cos (séries, exponentielle) qu'on voit en supérieur est donnée dans ce document.
Dernière modification par gg0 ; 02/07/2019 à 09h41.
Bonjour,
Je réalise le schéma, entre deux pauses et je pose ça dans la soirée. Ce sera effectivement plus clair avec un schéma, la démonstration étant essentiellement visuel.
sinon.
x n'est pas sur l'abscisse, c'est cos x. X c'est l'angle, le moment angulaire, de coordonnée (cosx, sinx). Je dessine tout ça cette après midi au propre, je scanne, car oui d'un point de vu géométrique, visuellement ça devient tout de suite plus évident.
Bonjour,
Voilà, ici on peut voir qu'avec un calcul d'aire, on démontre l'égalité.
ABCD, étant de même aire que A'B'C'D'. Et la hauteur H à la valeur de sin2x. On peut bien entendu le démontrer par calcul littéral, Pythagore, et où espace vectoriel, mais c'est moins intuitif.
