Bonjour
j'ai l'exercice suivant :
Question 2 : Décodage et application d’une méthode non vue mais apparentée :
La méthode dite «de la fausse-position » ou « regula-falsi » consiste à adapter la méthode
de bissection comme indiqué dans la figure suivante de la page suivante.
A partir de 2 valeurs a et b telles que f(a).f(b) <0 on procède comme suit :
0. Démarrage : x0 = a et x1 = b
1. à partir de xi et de xi+1 on détermine l’estimation suivante xi+2 en recherchant la
racine de la droite passant par les points (xi, f(xi) ) et (xi+1) ,f(xi+1))
2. On conserve ensuite, comme dans la méthode de bissection, l’intervalle qui
garantit l’existence d’une racine dans l’intervalle et on répète les étapes 1 et 2
jusqu’à obtenir une précision suffisante.
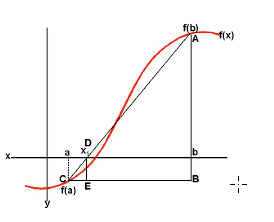
NB : sur ce graphe, le point noté C représente le point appelé ci-dessus (xi, f(xi)) ; le point
noté A , représente le point appelé ci-dessus (xi+1,f(xi+1)) et le point D représente le point de
coordonnées xi+2,0)
a) Déterminez l’expression de xi+2 en fonction de xi et de xi+1 à partir de la description de la
méthode donnée ci-dessus et en détaillant et justifiant votre développement. Comment
choisissez –vous l’intervalle à conserver ?
b) Utilisez l’expression obtenue pour calculer 3 étapes de cette méthode à l’équation de la
question 1 en partant de l’intervalle [0,1]. Pensez-vous que ce sera plus efficace que la
méthode de bissection ? pourquoi ?
c) Bonus : comparez les performances des différentes méthodes utilisées ou envisagées
pour rechercher les racines de l’équation de la question 1 et reliez vos constatations à la
théorie.
Je ne vois pas bien commencer le problème , pouvez m'aider merci
-----
. Tu n'as pas non plus vraiment lu ton énoncé qui dit "Déterminez l’expression de xi+2 en fonction de xi et de xi+1"; ce que tu ne fais pas; tu détermines même la valeur de p à partir de la valeur inconnue 