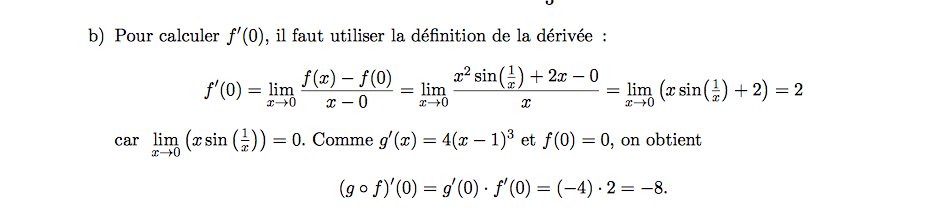Fonction dérivable, continûment dérivable

[FBMeca]

Bonjour,

Je ne sais si cet exercice a sa place dans la section "supérieur", veuillez m'en excuser si ce n'est pas la cas.

Je cherche à résoudre la question b) de ce problème.

Capture d’écran 2019-12-25 à 15.28.23.png

Ca fait pas mal de temps que j'étude les limites, la continuité, la dérivabilité, qui sont des notions très importantes et très liées. Or, j'ai un peu perdu toute notion d'ordre dans ma tête.
Prenons cette question : je me demande en quoi il est possible d'étudier la dérivée de cette composée en 0, si la fonction f n'est pas continûment dérivable en 0 (ce qui est bien juste j'espère, car le cos(1/x) nous embête). Si f(x) n'est pas continûment dérivable en 0, ca veut bien dire que la limite quand x -> 0 f'(x) n'est pas égale à f'(0). Or, ici on nous demande de calculer cette composée en 0, et je ne comprends plus très bien.

Une âme charitable pourrait-il m'éclaircir sur ce point. Et par ailleurs, une question un peu plus générale : comment déterminer si une fonction est dérivable et/ou continument dérivable ? Le problème est que je me perds souvent sur les limites, car on doit des fois utiliser la limite classique lim x->x0 f(x)-f(x0) / (x-x0) et dans d'autres circonstances tout simplement f'(x0)... cf. style d'exercice ci-dessous... Peut-être quelqu'un pourrait me rappeler et me définir ce que signifie être dérivable, continu, continûment dérivable (je peine à trouver des définitions claires et concises).

Capture d’écran 2019-12-25 à 15.38.16.png

Je vous en serais extrêmement reconnaissant !!

Déjà merci pour toutes vos réponses.

Bien à vous, et un joyeux Noël !
-----

[gg0]

Bonjour.

Tu poses des questions, mais tu ne dis rien de ce que tu as fait. As-tu regardé ce que fait cette fonction f en 0 ? Est-elle dérivable ?
Si oui, est-elle continument dérivable ? Si oui, pourquoi poser la question ? Si non regarde si gof est effectivement dérivable ou non en 0.
Si non, regarde si gof est effectivement dérivable ou non en 0.

Autrement dit, au lieu de poser les questions aux autres, pose-les toi à toi-même et fais le travail nécessaire.

Pour ta deuxième question, je suis un peu surpris que tu n'aies pas de définition claire et précise de "f est dérivable en x₀". C'est du cours de première, et on trouve partout cette définition (limite d'un quotient). "Continu", c'est du cours de base de première année post-bac, ou trouve la définition partout sur les cours de ce niveau. Donc tu n'as vraiment pas cherché et on ne va pas s'emm.. à écrire ici ce que tu peux trouver facilement toi-même. Dérivable sur l'intervalle I, c'est dérivable en tout x₀ élément de I, continument dérivable sur I, c'est dérivable sur I avec une dérivée continue sur I (*).
Dans l'exercice, les cours sur la dérivation (niveau première S) te permettent de voir facilement qu'elle est dérivable sur ]-oo, 0[ et sur]0,+oo[ et de calculer sa dérivée. Comme elle n'est pas définie par le même calcul en 0 (pour cause), tu ne peux plus utiliser la même méthode, et, intelligemment, tu vas utiliser la seule méthode qui te reste : la définition. Voilà pourquoi on utilise deux méthodes, c'est assez élémentaire.

NB : Ne perds pas ton temps à faire des exercices d'application sans avoir appris sérieusement les cours qui sont à appliquer. (**)

Cordialement.

(*) On utilise peut-être continument dérivable en x0, qui serait dérivable sur un intervalle ouvert contenant x₀ (un "voisinage de x₀") et de dérivée continue en x₀.
(**) j'enfonce des portes ouvertes, mais c'est bien ce que tu faisais, et tu n'es pas le seul ..

[FBMeca]

Bonjour,

Je trouve dommage que vous ayez pris ma question comme "un de ces étudiants qui veut tout simplement qu'on lui fasse l'exercice, puisqu'il est trop paresseux". J'ai fait plusieurs fois l'exercice, or certains détails semblent m'échapper, des détails tout de même importants, que j'aimerais comprendre, vous l'avez sûrement compris. Après, je peux comprendre que ma question puisse vous embêter, sur le coup j'essayais tout simplement d'obtenir de laide, d'où cette question un peu (trop?!) générale ; prenez-le à la légère...

Je ne sais pas comment faire pour rédiger, ce que j'ai fait, ici sur le forum.

Bref.. merci pour votre temps ?!

Cord.

[ansset]

bjr, il me semble que tu ne donnes pas l'énoncé complet.
les seules questions lisibles sont "calculer les dérivées de...".
ensuite tu évoques le souci en x=0 pour la deuxième fonction.
effectivement il y en a un ( qui mérite réponse ).... mais ceci est présenté :

Or, ici on nous demande de calculer cette composée en 0, et je ne comprends plus très bien.

je doute que ce soit l'intitulé de la question.

enfin, nul part il semble être question de "continuement dérivable" .

peut on avoir l'exercice , et surtout les questions posées ?

[A voir en vidéo sur Futura]

[ansset]

pour le dire autrement, il y a une différence entre :
voici une fonction : calculer sa dérivée ( question générale )..... et
étudier la dérivabilité de cette fonction en x=x0 .

elle peut y être dérivable, non dérivable, dérivable par continuité.....

[gg0]

Non, je ne t'ai pas pris pour "un de ces étudiants qui veut tout simplement qu'on lui fasse l'exercice, puisqu'il est trop paresseux". Je l'aurais dit. Simplement, tes questions sont trop vagues pour autre chose que ce que j'ai ressenti et donc écrit. Tu dis que tu as "fait plusieurs fois l'exercice", mais rien de ce que tu as trouvé. On ne peut pas t'aider à rédiger une question pour laquelle on n'a pas tes tentatives de traitement. Comme on n'avait rien de tout ça, j'ai essayé de te donner des pistes.
Mais si tu ne veux pas répondre à mes questions faites pour t'aider, tant pis...
Sinon, tu peux soit écrire en LaTeX (voir le fil sur LaTeX), soit prendre un scan ou une photo d'un texte bien écrit (ce sera plus long, il faut attendre la validation par un modérateur du forum).

Cordialement.

[FBMeca]

Bonjour,

Oui tout à fait, la première capture présente l'ensemble de l'exercice. Mes questions sont par rapport à l'énoncé b) de l'exercice. La deuxième capture n'a rien à voir avec cet exercice, oubliez-le pour l'instant.
On nous demande de calculer (g o f)' en 0.
Or, ce que je ne comprends pas, c'est qu'on nous demande de calculer cette valeur, alors que, si on analyse la fonction f, on voit qu'elle n'est pas continûment dérivable. Est-ce que ceci ne veut pas dire que lorsqu'on veut calculer la valeur de f' en 0, elle sera différente quand x->0 comparé à quand x = 0 ?

Je ne sais pas si je suis clair, excusez-moi...

[FBMeca]

Bonjour gg0,

Je vous remercie pour votre aide, or je vous l'avoue, vous avez été trop direct et je ne trouve plus vraiment l'envie de trouver réponse à ma question. Pourquoi pas tout simplement me répondre "peux-tu reformuler ta question, qui est trop vague ?" ? Je suis tout de même d'avis que ma question nécessite pas un développement très complexe, je ne pense pas avoir besoin de prendre 45 minutes pour poser une question, qui peut sembler vague, d'une autre manière.

Je vais essayer de reformuler ma question : prenez la première image, question b). On nous demande de calculer la valeur de (f o g)'. Par contre, moi ce que je vois, c'est que la dérivée de f n'est PAS continue en 0 (il suffit de calculer les limites, un cos(1/x) reste qui oscille, donc aucune limite). Est-ce bien juste ?
Si oui, voici ma question : pour calculer (f o g)', il nous fait f'(0). Mais ici, avant même de faire le calcul, on vient de voir que lim x-> 0 f'(x) n'est pas égal à f'(0). Est-ce bien juste ?
Si oui, comment est-on censé calculer (f o g)' en 0 si f'(0) n'est pas vraiment d'une forme que l'on souhaite, à savoir quelque chose qui est égal partout dans un voisinage ?
Ou bien est-ce qu'on s'en fiche de savoir que vaut lim x-> 0 f'(x) ?

J'espère avoir été plus clair.

Merci d'avance!

[ansset]

effectivement , la "calculer" en 0 est inapproprié car la fct n'y est pas dérivable.
et la dérivée de la fonction n'a même pas de limite +/- l'inf en ce point.

[FBMeca]

Mais c'est bien ce qu'on me demande dans l'exercice 10 b) (première capture) !? Que suis-je censé faire, je ne comprends plus très bien ?

[gg0]

"Si oui, voici ma question : pour calculer (f o g)', il nous faut f'(0)." Pas nécessairement, c'est ce que j'ai essayé de te dire (*). Pour appliquer la formule de dérivation d'une composée de fonctions dérivables, oui, il faut que f'(0)existe.
Donc ton problème est bien de savoir si f est dérivable en 0. Tu recules sous prétexte que f' n'est pas continue en 0. Est-ce dans le théorème ? Pas dans le mien, en tout cas. Seules les existences des dérivées de f en 0 et de g en f(0) sont demandées.

Comme on a besoin d'être clair, d'avoir des références sur ces questions parfois délicates, il te faut un cours utilisable (bouquin de licence/prépa, pdf d'un prof sérieux, ..), le lire, apprendre les principaux résultats, et t'y référer. Poser des questions sur des forums ne construit pas un savoir solide.

Cordialement.

(*) f et g pourraient être non dérivables et gof être dérivable. Ou seulement f non dérivable (f est l'indicatrice des rationnels, et g la fonction constante égale à 1).

[ansset]

de dire que tel que posé , la dérivée de g(f(x)) n'est pas calculable en 0.
mais c'est aussi lié à g(x).
si g(x)=x^4 et non (x-1)^4 , on a une réponse différente.

[FBMeca]

Je trouve ca tout de même étrange, car le corrigé que j'ai, je peux vous l'envoyer si ca peut aider (dites-le moi), stipule qu'on peut faire le calcul sans souci et donne une réponse (-8 je crois...). Si je suis censé trouver une réponse, comment dois-je faire ? Prendre lim x->0 de f'(x) et utiliser la définition de la limite (lim x->x0 de f(x) - f(x0) / x - x0) ?
Très intéressant, mais pourquoi est-ce que avec ce g(x) précis ce serait plus précis ? Et précis dans quel sens ?

Merci encore!

[gg0]

Pour l'exercice 10, b, on a f'(0) = 2, g'(x)=4(x-1)^3, donc g'(f(0))=g'(0) =-4, donc(gof)'(0) = 2*(-4)=-8. C'est tout ! On applique le théorème.

Le cours, toujours connaître le cours.

[ansset]

oui, avoir le corrigé serait bien.
j'espère qu'ils n'ont pas fait la dérivée de f(g(x)) ! ( mais ça ne donne pas -8 )

quand à l'autre g(x) que je propose, relis ce qu'a écrit gg0.

[gg0]

Heu ...Ansset, on parle de l'exercice 10 ( premier document) depuis le message #7 ("La deuxième capture n'a rien à voir avec cet exercice, oubliez-le pour l'instant.")

Cordialement.

[ansset]

Pour l'exercice 10, b, on a f'(0) = 2, g'(x)=4(x-1)^3, donc g'(f(0))=g'(0) =-4, donc(gof)'(0) = 2*(-4)=-8. C'est tout ! On applique le théorème.

Le cours, toujours connaître le cours.

évidemment.....

[FBMeca]

Je vous remercie pour votre aide, et je suis d'accord avec ce que vous dites. Mais mon corrigé, ni mon cours, vont me donner réponse à toutes mes questions...

Voici le corrigé, il fait exactement ce que vous faites. Le théorème nous dit donc qu'on doit prendre lim x -> 0 pour f'(0) ? Enfin, puisqu'elle n'est pas continue...Je pense que ce que je ne comprends peut-être pas est pourquoi il est écrit : "il FAUT utiliser la définition de la dérivée..." ?!

[ansset]

ps pour FBMeca :


c'est ça "il FAUT utiliser la définition de la dérivée".

[FBMeca]

Mais le f'(0) quand x=0, n'est-il pas tout simplement égal à 0 si la fonction est définie ainsi ?

Ah, maintenant je dis plus que des bêtises. Je crois avoir pensé que, puisque f(0) = 0, f'(0) était aussi = 0. Ce qui est n'importe quoi, nous sommes bien d'accord ?

[FBMeca]

Dernière question, et alors quand sommes-nous pas obligés d'utiliser la définition de la dérivée ? ...

[gg0]

Quand on n'a pas d'autre méthode (voir mon premier message).

Et ne pas confondre f'(a) et lim f'(x) quand x tend vers a. C'est f qui est continue quand elle est dérivable, f' peut très bien être discontinue.

[gg0]

Voir cependant le théorème de prolongement de la dérivée.

[FBMeca]

Un grand merci pour votre aide, gg0 et ansset, c'est beaucoup plus clair à présent !

Très belle soirée à vous deux !