Bonjour
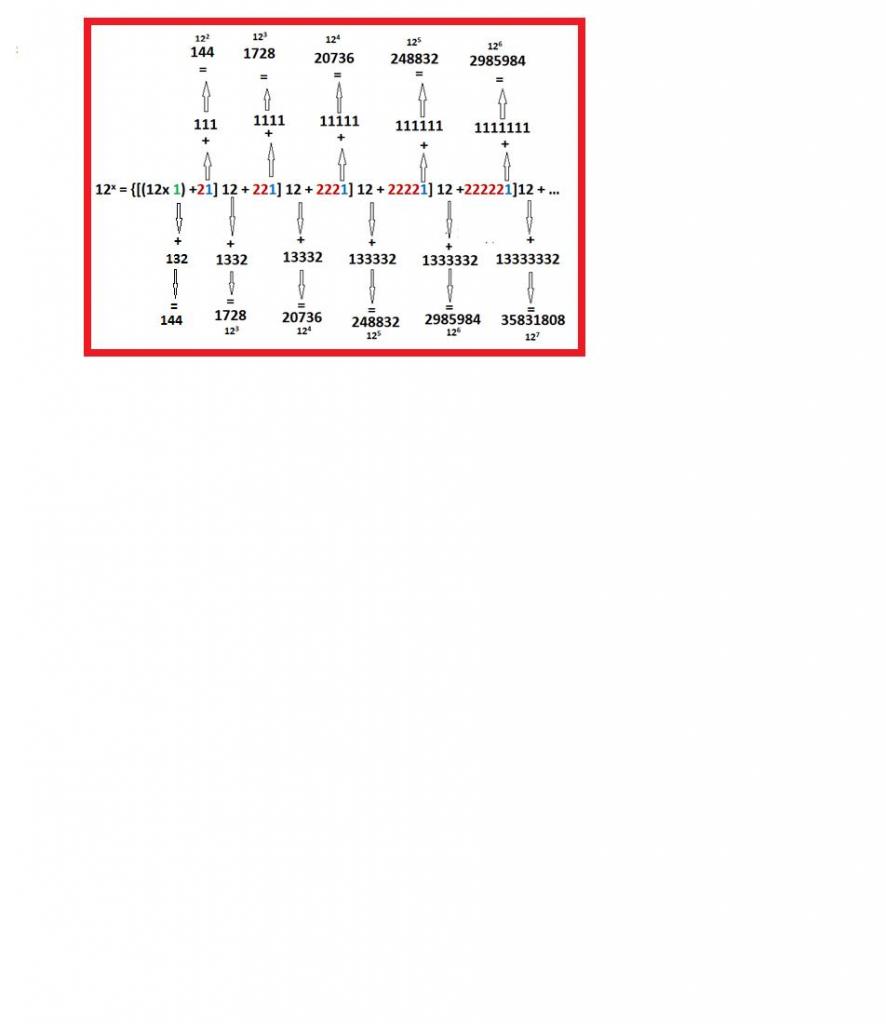
une nouvelle méthode de calcul de la puissance des entiers naturels permet de vérifier la méthode habituelle qui consiste à multiplier N par lui même.
Qui diffère cette méthode de l'autre c'est que le chiffre de départ ne quitte pas le déroulement des opérations. Par exemple 13 puissance 6 par l'ancienne méthode c'est 13 x 13 = 169 puis 169 x 169 = 28561, puis 28561 x 169 = 4826809 alors que par cette méthode c'est 1444443 + 144443 x 2 + 12 x 13 x 1269; le chiffre de départ 13 est presque toujours présent.

-----