Bonjour à tous,
Dans un problème de mécanique je me retrouve à devoir résoudre une équation différentielle de la forme y' = Ay + By² + Cy3 + D où A, B, C et D sont des constantes. Je sèche totalement sur la méthode de résolution, est-ce résolvable "manuellement" ou une méthode numérique est nécessaire ?
Merci d'avance pour votre aide.
Facile ça revient à trouver les primitives d'un polynômes. Ou je suis rouillé.
C'est très certainement moi qui suis rouillé. Est-ce que vous pourriez me détailler un peu la méthode ?
Merci !
Ben tu connais la primitive s'annulant en 0 de a*1, de a*x, de a*x² etc. ? C'est respectivement a*x, a*1/2 * x², à*1/3*x³ etc.
Bonjour,
Hum ! 2ème optionEnvoyé par Merlin95
Quand on a un doute, on peut toujours essayer avec un exemple et wolframalpha : https://www.wolframalpha.com/input/?...2B+y%5E3+%2B+1
C'est une équation à variables séparables,ça s'intègre de façon classique une fois la décomposition de la fraction rationnelle en éléments simples effectuée.
Donc, ça se résout si on a des valeurs précises de A, B, C, D. Sinon, dans le cas général, une fois l'intervalle d'étude précisé, on ne peut pas en dire tellement plus (il faut que le dénominateur ne s'annule pas, précaution habituelle, et on peut avoir des solutions différents sur chacun des domaines où la fraction est définie + voir éventuellement comment elles se raccordent).
Not only is it not right, it's not even wrong!
Oui en effet j'ai mélangé variables fonction, désolé.
J'aurais fait grincer des dents à bien des profs de maths, ça j'aurais du le voirC'est une équation à variables séparables
J’espère pour vous que ce polynôme en Y a au moins une racine évidente, car sinon, faut se tartiner une équation de degré 3, ce n'est pas le plus simple.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Malheureusement pas de racine évidente, j'ai utilisé Wolframalpha pour la résolution de l'équation et je dois dire que le résultat n'est pas drôle, et à base de complexes en plus ce qui ne m'arrange pas trop pour une application "mécanique".J’espère pour vous que ce polynôme en Y a au moins une racine évidente, car sinon, faut se tartiner une équation de degré 3, ce n'est pas le plus simple.
Merci pour votre aide !
Bonjour.
A priori, il y a au moins une racine réelle, et Wolframalpha doit la donner. Ce qui permet de factoriser le dénominateur pour faire la décomposition en éléments simples réelle et d'intégrer.
N'importe comment, on obtient finalement x en fonction de y, et pas vraiment ce qu'on veut. l'inversion de la fonction x=g(y) peut être à elle seule aussi compliquée que tout le reste, voire impossible algébriquement.
Cordialement.
Pardon je me suis mal exprimé, je voulais dire que j'avais directement utilisé Wolframalpha pour la résolution de l'équation différentielle.A priori, il y a au moins une racine réelle, et Wolframalpha doit la donner. Ce qui permet de factoriser le dénominateur pour faire la décomposition en éléments simples réelle et d'intégrer.
N'importe comment, on obtient finalement x en fonction de y, et pas vraiment ce qu'on veut. l'inversion de la fonction x=g(y) peut être à elle seule aussi compliquée que tout le reste, voire impossible algébriquement.
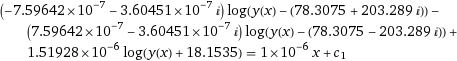Avec des valeurs, l'équation est donc y' = 0.000013y^3 - 0.0018y^2 + 0.58y + 11.2, et la solution donnée par Wolframalpha estce qui m'embête car je ne sais pas comment interprêter la partie imaginaire d'un point de vue mécanique.
A priori,
l'équation donnant x en fonction de y a bien toujours une solution réelle(pas très agréable), et deux solutions complexes sans intérêt sans doute dans ton problème. Wolfram fait du calcul formel, applique ses procédures, qui ici ne donnent pas la bonne solution. C'est un des cas où il faut parfaitement connaître les logiciels qu'utilise Wolfram pour pouvoir éviter ce piège.
Voici la solution réelle de 0.000013y^3 - 0.0018y^2 + 0.58y + 11.2 = 0 qui permet de le factoriser
-20/39*(10099350+1950*56733339^(1/2))^(1/3)+323000/13/(10099350+1950*56733339^(1/2))^(1/3)+600/13
En valeur approchée pour une résolution approchée (risquée !) : -18.15351298.
Et la factorisation : 0.000013y^3 - 0.0018y^2 + 0.58y + 11.2=(y+18.15351298)(0.000013* y^2-0.002035995669*y+0.6169604738)
En redéveloppant, on voit que seul le 11.2 est approché (11.19999997).
Cordialement.
NB : j'ai évidemment utilisé un logiciel de calcul formel, mais il ne sait pas mieux résoudre cette équation différentielle exactement.
Super, merci beaucoup pour votre aide ! Maintenant qu'il y a cette factorisation il faut développer en éléments simples pour intégrer c'est bien ça ?A priori,
l'équation donnant x en fonction de y a bien toujours une solution réelle(pas très agréable), et deux solutions complexes sans intérêt sans doute dans ton problème. Wolfram fait du calcul formel, applique ses procédures, qui ici ne donnent pas la bonne solution. C'est un des cas où il faut parfaitement connaître les logiciels qu'utilise Wolfram pour pouvoir éviter ce piège.
Voici la solution réelle de 0.000013y^3 - 0.0018y^2 + 0.58y + 11.2 = 0 qui permet de le factoriser
-20/39*(10099350+1950*56733339^(1/2))^(1/3)+323000/13/(10099350+1950*56733339^(1/2))^(1/3)+600/13
En valeur approchée pour une résolution approchée (risquée !) : -18.15351298.
Et la factorisation : 0.000013y^3 - 0.0018y^2 + 0.58y + 11.2=(y+18.15351298)(0.000013* y^2-0.002035995669*y+0.6169604738)
En redéveloppant, on voit que seul le 11.2 est approché (11.19999997).
Cordialement.
NB : j'ai évidemment utilisé un logiciel de calcul formel, mais il ne sait pas mieux résoudre cette équation différentielle exactement.
Aussi, quel est le logiciel que vous avez utilisé ? Si jamais je dois refaire les calculs, que je sois à peu près autonome.
Merci !
J'ai utilisé Maple, mais tu aurais pu faire ça sur Wolfram, basé essentiellement sur Mathématica. Ou télécharger Xcas, qui est gratuit.
Merci pour ces précisions.
Du coup, je devrais décomposer la fraction 1/(0.000013y^3 - 0.0018y^2 + 0.58y + 11.2) en une somme de fractions de la forme A/(y+18.15351298) + (Bx+C)/(0.000013* y^2-0.002035995669*y+0.6169604738) c'est bien ça ? Je maitrise assez peu la décomposition en éléments simples, donc je préfère demander conseil.
Merci !
Oui, c'est cela.
Puis intégrer, obtenir x en fonction de y, puis inverser la fonction x=f(y).
Et comme déjà les valeurs sont des approximations, le résultat sera encore plus approximatif.
Super merci pour cette confirmation. J'ai bien conscience de l'approximation du résultat mais faute de mieux, c'est déjà ça !Oui, c'est cela.
Puis intégrer, obtenir x en fonction de y, puis inverser la fonction x=f(y).
Et comme déjà les valeurs sont des approximations, le résultat sera encore plus approximatif.
Encore merci pour votre aide.
