Calcul de centre de gravité d'un solide

[Lebuis]

Bonsoir
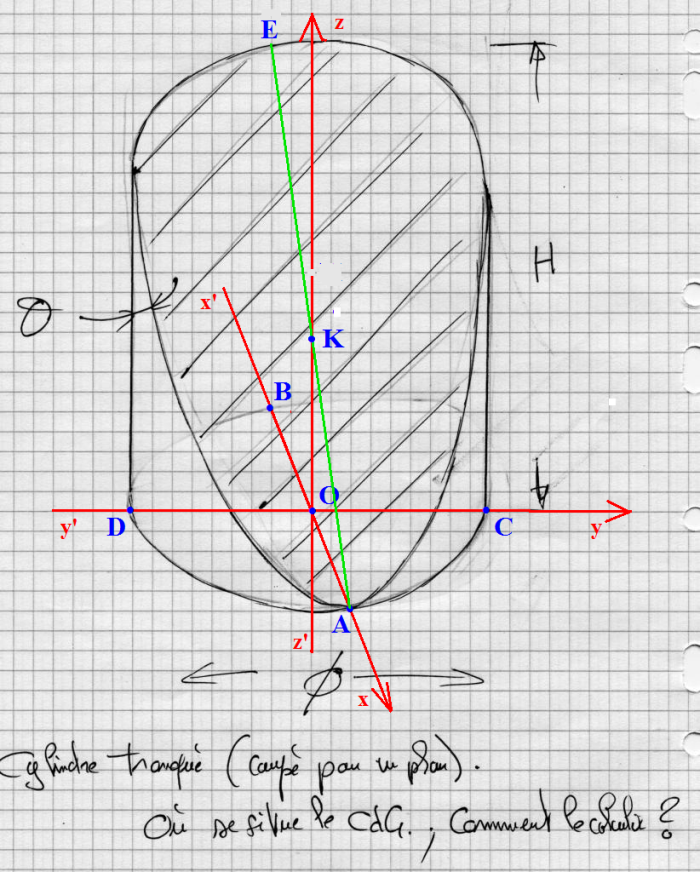
Je dois trouver le centre de gravité d'un cylindre tronqué par un plan.
On se donne toutes les cotes (variables). voir P.J.

Merci de votre aide. Indiquez moi svp la démarche voire le développement afin que je progresse dans mes recherches.

Bien cordialement
Merci à celles et ceux qui savent et qui aident.

LEBUIS
-----

[jacknicklaus]

Bonjour,

je crains qu'il faille sortir l'artillerie lourde.


Où O est l'origine d'un repère, G le barycentre, V le volume total (voir google pour la formule connue d'un cylindre coupé par un plan), où M parcours tout le volume, et dv le volume infinitésimal au point M.
Pour aller au plus simple, raisonner en considérant le dv comme une tranche fine d'épaisseur dz, calculer sa surface en fonction de z (faire un dessin), et intégrer sur z. A vue de nez, je pense qu'il est préférable de prendre des coordonnées cartésiennes (à cause de l'équation du plan de coupe)

[Opabinia]

Bonjour,

Le choix d'un repère approprié est indispensable à un bon départ des calculs.

Le solide étudié est délimité:
a) par le plan horizontal (xOy) d'altitude nulle (z = 0);
b) par le cylindre vertical d'axe (z'z), s'appuyant sur le cercle de centre (O) et de rayon

R = OA = OB = OC = OD ;

c) par l'ellipse de centre K (0, 0, H/2) et de grand diamètre (AE), ce dernier point ayant pour coordonnées:

(-R, 0, H) .

[jacknicklaus]

Tous calculs faits, un peu pénibles, et en notant H la hauteur et D le diamètre, je trouve que le barycentre est à la hauteur

et à la distance de l'axe (vers la partie pleine, bien entendu)


C'est du pur calcul intégral sans le moindre intérêt. Je n'ai pas vu d'astuce permettant d'y échapper.
Je laisse le PP indiquer s'il trouve la même chose, et à fournir ses calculs si besoin.

[edit]
faire F5 rafraichissement de page pour afficher le Latex, il semble qu'il y ait des problèmes.

(y'en a qu'ont essayé, ils ont eu des problèèèmes)

[A voir en vidéo sur Futura]

[Lebuis]

Bonjour Jacknicklaus
Merci pour votre réponse.
Questions :
Pourquoi les coordonnées du CG ne dépendent pas d''alpha , angle d'inclinaison du plan coupant le cylindre ?
Pourrais je avoir un scan de vos calculs svp ?

Merci
Bien cordialement
Lebuis

[gg0]

Elles en dépendent, z en tout cas.

Cordialement.

NB : Jacknicklaus attend que tu fasses toi-même les calculs (règlement du forum !!)

[jacknicklaus]

Pourquoi les coordonnées du CG ne dépendent pas d''alpha , angle d'inclinaison du plan coupant le cylindre ?

parce que H, D, et alpha sont redondants. En effet D/H = tan(alpha), donc H et D suffisent pour caractériser les dimensions.

Pourrais je avoir un scan de vos calculs svp ?

Sur ce forum, on est supposé aider à trouver des solutions, pas les donner toutes faites.

Je t'ai donné une piste avec la formule du poste #2.
A toi de la suivre et d'indiquer ce qui te bloque pour la mettre en application. Alors, on t'aidera.