Résoudre une équation en a*t-b*sin(PI*t)=k

[zedrummer]

Bonjour
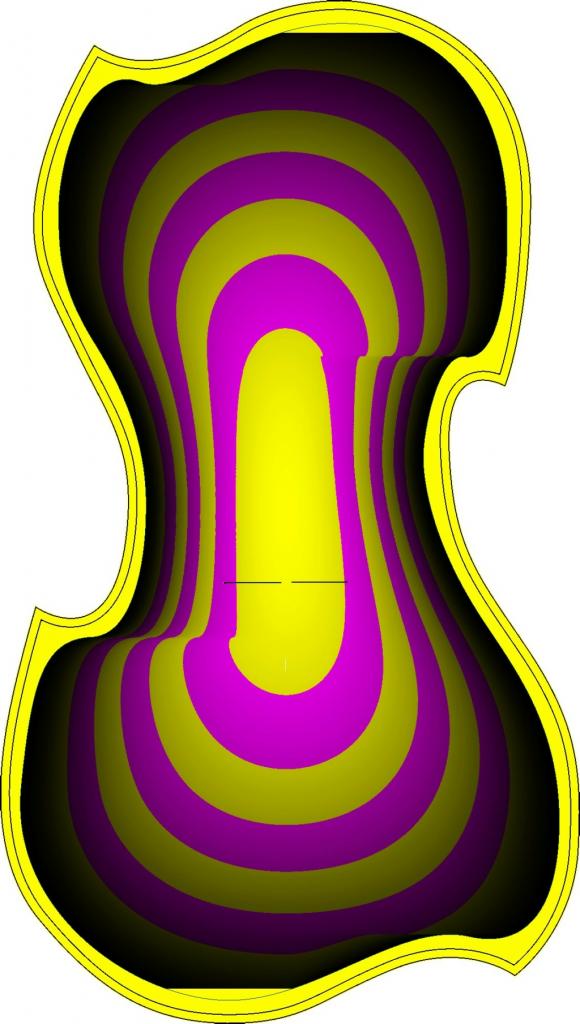
Il y a quelques temps je postais sur mes débuts de luthier amateur dans le monde du quatuor. Pour cette activité, j'ai développé un programme en C à qui je fournis une image du contour d'un violon et qui doit me produire des courbes de niveaux pour la sculpture de la voûte de la table et du fond.
Grâce à votre aide, j'avais réussi à ce que ce programme marche et j'ai depuis réalisé un violoncelle puis un violon:

img_2066.jpg

img_2076.jpg

Maintenant, souhaitant améliorer encore le programme, j'ai appris depuis que si l'on veut modéliser la voûte de manière mathématique, il faut utiliser des trochoïdes raccourcies.
Je suis donc avec ces formules (avec t dans [0;1]):

x=LongueurVoute*(t-sin(PI*t)/(2*PI))
y=HauteurVoute/2*(1-cos(PI*t))

Le truc, c'est que pour produire mon image finale avec les courbes de niveaux, je suis obligé de remplir chaque pixel dans le plan XZ avec des valeurs/couleurs dépendant de la hauteur Y.
Je suis donc obligé de savoir le plus précisément possible pour tel x quelle est la valeur de t correspondante et là je sèche:
Est-ce possible et, si oui, comment résoudre une équation de type a*t-b*sin(PI*t)=k où a, b et k sont des constantes, SVP?
Pour l'instant je fais par tâtonnement sur la valeur de t, mais forcément niveau efficacité et précision, ce n'est pas fameux.

Merci
David
-----

[gg0]

Bonjour.

Si tu connais a, b et k, il y a des méthodes élémentaires de résolution approchée. Résolution approchée parce qu'il n'y a pas de calcul algébrique pour donner les solutions. Scilab peut te faire cela facilement, ou Xcas, mais ces deux logiciels gratuits nécessitent un apprentissage. Sinon, une simple calculette graphique (ou logiciel traceur de courbe) te permet de représenter a*t-b*sin(PI*t) sur [0;1], puis faire des zooms successifs sur la zone où ça vaut à peu près k. On obtient facilement et rapidement la valeur approchée de t à 4 ou 5 chiffres significatifs exacts.

Cordialement.

[jacknicklaus]

Bonjour,

deux exemples de méthodes de résolution numériques bien connues. Faire des essais dans ton cas précis pour voir la plus efficace.

https://fr.wikipedia.org/wiki/M%C3%A..._de_dichotomie

https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Newton

[zedrummer]

Hello gg0 et merci de ta réponse

En fait, le but est d'intégrer le calcul à mon programme et il fait déjà une résolution approchée, mais ça rend le programme relativement lent, forcément. Ma méthode pour l'instant est de calculer x avec t sur des intervalles les plus petits possibles. Je pourrais rajouter le fait de faire ensuite des pas encore plus petits à l'intérieur de l'intervalle précédent, mais là ça va devenir l'enfer.

Une amélioration serait sans doute de déjà remplir un bloc mémoire avec des valeurs pré-calculées sur les premiers intervalles, puis de calculer sur les intervalles plus petits, mais ma question était bien "est-ce qu'il est possible de résoudre cette équation?". Donc non.

Merci encore d'avoir pris le temps de répondre
Cordialement
David

[A voir en vidéo sur Futura]

[zedrummer]

Hello jacknicklaus et merci de ta réponse
Du coup, j'étais effectivement parti sur la dichotomie, mais je ne connaissais pas la méthode de Newton, je vais regarder ça.
Merci encore
Cordialement
David

[Black Jack 2]

Bonjour,

Si tu veux aller très vite ... et que tu disposes de places en mémoire.

Tout dépend évidemment de ce que tu entends par "le plus précisément possible pour tel x quelle est la valeur de t correspondante"

Tu fais un tableau (précalculé) en mémoire avec (t-sin(PI*t)/(2*PI)) en entrée (adresse) et t en sortie (valeur contenue dans la position de mémoire)

(t-sin(PI*t)/(2*PI)) varie dans [0 ; 1].
Si tu fais un tableau de 1000 places (par exemple), tu calcules (x/longueur de voûte) et tu vas chercher dans le tableau le [ent(1000 * (x/longueur de voute))] item ... qui te sort la valeur du t correspondante.

Voir si la précision est suffisante ... sinon adapter la quantité de cases mémoires pour le tableau.

[zedrummer]

Hello Black Jack 2
Merci de ta réponse qui effectivement va me faire gagner du temps, je ne l'avais pas pensé ainsi, surtout que je peux aller bien au delà de 1000 places qui même si c'est du type "double" ferait moins de 8ko. Je pourrais sans problème allouer 1000 fois plus et avec 1 million de valeur, je serais sans doute assez précis, même pour des images de 5000 pixels.
Merci beaucoup à vous tous

[obi76]

Bonjour,

En fait, le but est d'intégrer le calcul à mon programme et il fait déjà une résolution approchée, mais ça rend le programme relativement lent, forcément.

Si c'est correctement codé (et en C), ça peut être extrêmement rapide, c'est le genre de problème que j'ai déjà eu et en un temps raisonnable avec une (excellente) résolution, ça se fait

Après vous pouvez faire une méthode mixte : vous avez un tableau pour pré-encadrer la valeur que vous cherchez, puis vous faites quelques itérations (Newton ou dichotomie) pour converger à la précision voulue sur la valeur que vous voulez

[invite23cdddab]

Sachant qu'avec la méthode de Newton, la précision double à chaque itération, en général, il ne suffit que 4-5 itérations (voir moins) pour avoir une précision acceptable.



Par exemple, pour a = 27.34, b = 12.78, k=5, les premières itérations sont :

= 0
= 0.074085539
= 0.074488849
= 0.074488885

Et on est déjà à 8 décimales correctes en 3 calculs simples (si t est en mètres, la précision est de l'ordre de la dizaine de nanomètres... soit la taille de quelques atomes)

[zedrummer]

Merci à vous 2, effectivement, la définition est largement suffisante, on est plus de l'ordre du millimètre que du mètre, donc...

[zedrummer]

J'ai un souci: la méthode de Tryss2 marche très bien sauf quand on commence à se rapprocher des grandes valeurs!
Avec ma formule
x=LongueurVoute*(t-sin(PI*t)/(2*PI))
Si je lance 4 itérations pour LongueurVoute=800 (en pixels), jusqu'à x=650 c'est très correcte, il me rend le bon t (si je recalcule avec la fonction ci-dessus, je suis très proche du x donné), par contre au delà, ça part complètement en couille, la valeur devient complètement fausse et le x s'effondre revenant vers 0. En augmentant le nombre d'itérations, ça a l'air de s'améliorer, mais quoi qu'il arrive, ça finit par faire n'importe quoi quand on se rapproche de 800.

[invite23cdddab]

Du coup, part plutôt de , tu va éviter le problème

[invite23cdddab]

En fait, ce qu'il se passe ici, c'est qu'en partant de 0, la méthode de Newton fait presque un cycle dans ce cas (voir un véritable cycle si x = Longueur voute).

Si on veut résoudre f(t) = 0.5 en partant de t=0, la représentation graphique de la méthode de Newton ressemble à ça :
NewtonGood.png

On voit que l'on arrive très vite proche de la solution.

Par contre, si on veut résoudre f(t) = 0.99 en partant de t=0, ça ressemble à ça :
NewtonBad.png

Les valeurs vont osciller entre des nombres très proches de 0 et très proches de 2 pendant un moment...

En partant de 1, on n'a pas ce problème si on veut résoudre f(t) = k pour k entre 0 et 1

[zedrummer]

Ah d'accord, je comprends, du coup là effectivement, ça marche au poil, merci infiniment!