Conjecture nombre premiers

[extrazlove]

Bonjour à tous,


Je cherche à vous présentez une approche, pour trouver la distribution des nombres premiers dans l'ensemble des entiers.
Je cherche à savoir si on a déjà pensé à cette approche et votre critique sur cette approche.


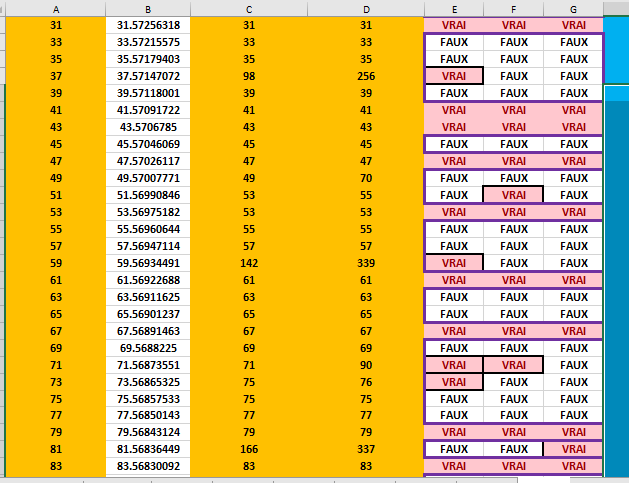
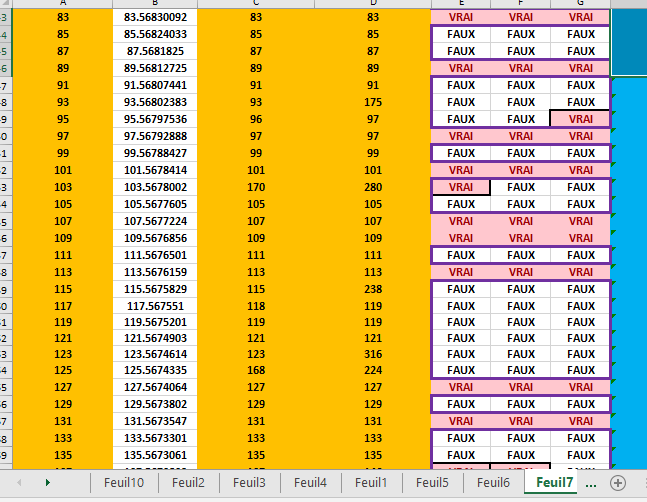
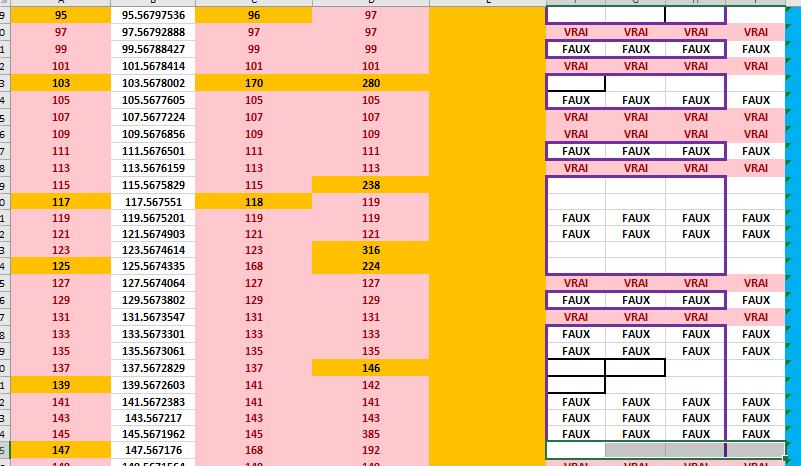
Soit la série Un=n et soit Vn=f(Un) avec n un entier et f une application.
La séquence U0, U1,U2, ..., Un contient p nombre premiers.
La séquence V0,V1,V2, ..., Vn contient k nombre premiers.


J'ai trouvé un exemple de Vn croissante qui donne k ~ 1.5*p sous Excel.


Et à la place de chercher une logique de nombre premiers dans la liste U0, U1,U2, ..., Un, je vais plutôt chercher une logique entre nombre premiers dans la liste V0, V1, V2, ..., Vn où il y a plus de nombre premiers dans cette liste.


Si je trouve cette logique, je peux écrire k en fonction de n, puis p en fonction de n, pour trouver une logique de la distribution de nombre premiers dans l'ensemble des entiers.
Voici un pdf qui montre avec un exemple de Un et Vn

Que Vn est premiers si Vn-1, Vn, Vn+1 sont tous différents.

Et que la somme des nombres premiers dans la suite Un plus la somme des premiers de Vn est différent de la somme de la somme de Vn.
-----

[extrazlove]

Voici je peux formuler une conjecture sur les nombres premiers:

Soit Un et Vn deux suites croissante d'entiers et Vn>Un qui sont définies sur le pdf envoyé.
et up et vp la somme de quantité des nombres premiers jusqu'à n,

Par exemple il y a 2 3 5 qui sont premiers dans Un donc u5=1+1+1=3 et v5=4 car il y 4 nombre premiers jusqu'à 5 dans Vn.


La conjecture dis si un est unique(ne se répète qu'une seule fois) dans la liste des sommes premiers de Un(u0,u1,u2..un) et Un+Vn( u0+v0,u1+v1,u2+v2..un+vn) alors Vn est premiers.

Peut on démontrer ou réfuter cette conjecture?

[extrazlove]

Avec cette conjecture je peux même estimé où se trouve un nombre premiers grand, surtout que je connais la distribution de nombre premiers pour évaluer la somme de Un et la somme de Vn~1.5 la somme de Un.

[extrazlove]

Bonjour,

Par exemple pour:
Zn=((n*(1+LOG(U_n)-LOG(U_n+1))+1))
Vn=ENT(Z_n+1*(EXP((SIN(Z_n+2-U_n+2)^2)^Z_n+3-(COS(U_n+2+Z_n+2)^2)^Z_n+3)))
et Un=n.

J'observe que les positions des nombres premiers sur Un et Vn sont pareil pour les valeurs ou Un=Vn.

Et quand Un#Vn la positions de n indique ou il y a des valeurs de Un et Vn qui ne sont pas premiers.

[A voir en vidéo sur Futura]

[extrazlove]

Voici un exemple :

Puisque les nombres premiers représente l'unité,je m'attaque a l'unité pour trouver une distribution possible de nombres premiers, en clair si n est premiers alors Vn est premiers si ils ont la même unité Vn=n.

Si n#Vn on ne peut pas juger, mais on peux éliminer ce cas de figure.

J'observe que les positions des nombres premiers sur Un et Vn et Dn.. sont pareil pour la majorités des valeurs .

La majorité des nombres premiers reste fixe dans la suite Un et Vn et Dn... et les autres nombres non premiers change avec le choix de Vn et Vn... d'où en peux trouver une distribution possible qui passe par des nombres premiers fixe sur Un et Vn et Dn..

Voici en image comment je veux retrouvez une distribution de nombre premiers.

Je cherche La fonction qui élimine tous les valeurs qui change et gardent que les nombres statistiques qui sont premiers et je peux utiliser autant de suites possibles pour voir ou sont les nombres premiers et éliminer les cases qui contiennent un faux en engendrant une valeur non répétitive pour éliminer les max des case possibles.

On peux observer que n est premiers si Vn=Un=Dn.. si non n est entier.

et que si on a des nombres qui ne se répète pas sur (Un Vn Dn...) on peux éliminer des lignes et raccourcir la position des nombres premiers.

Pour trouver un P=17217086869046677 il faut calculer juste ou ...Un-1 et Dn-1 et Vn-1 Un et Dn et Vn puis Un+1 et Dn+1 et Vn+1… ou sont égale pour trouver n+k ou n-k premiers et on trouver beaucoup de valeur unique pour éliminer les nombres non premiers de la liste.

Par exemple pour n=1721715 pour trouver que n=1721718 on a Un=Vn=Dn=An=Bn=Cn=....pour faire autant des valeurs qui ne se répète pas pour trouver un p+k ou p-k premiers .

Peut être si on connais juste n, on peut estimer les suites à choisir Vn Dn... pour donner beaucoup des valeurs répétitives autour de n pour trouver la position de nombre premiers le plus proche n+k ou n-k, on vérifiant simplement que Un=Vn=Dn et qui il y des valeurs non répétitive entre n-k ou n+k.
La on cherche pas la probabilité de présence de nombre premiers on choisi juste Vn et Un et Dn qui vont bouché tous les lignes ou il y plus d'un faux puis on calculé si Vn+k=Dn+k=Un+k n+k ou n-k sera premiers.

[extrazlove]

Voici les images .

[jacknicklaus]

J'observe que les positions des nombres premiers sur Un et Vn sont pareil pour les valeurs ou Un=Vn

Quant à moi, j'observe que n'importe quel couple de propriétés dépendant l'une de Un, l'autre de Vn, "sont pareils pour les valeurs où Un = Vn".

[albanxiii]

Contournement d'une décision de modération => fermeture.