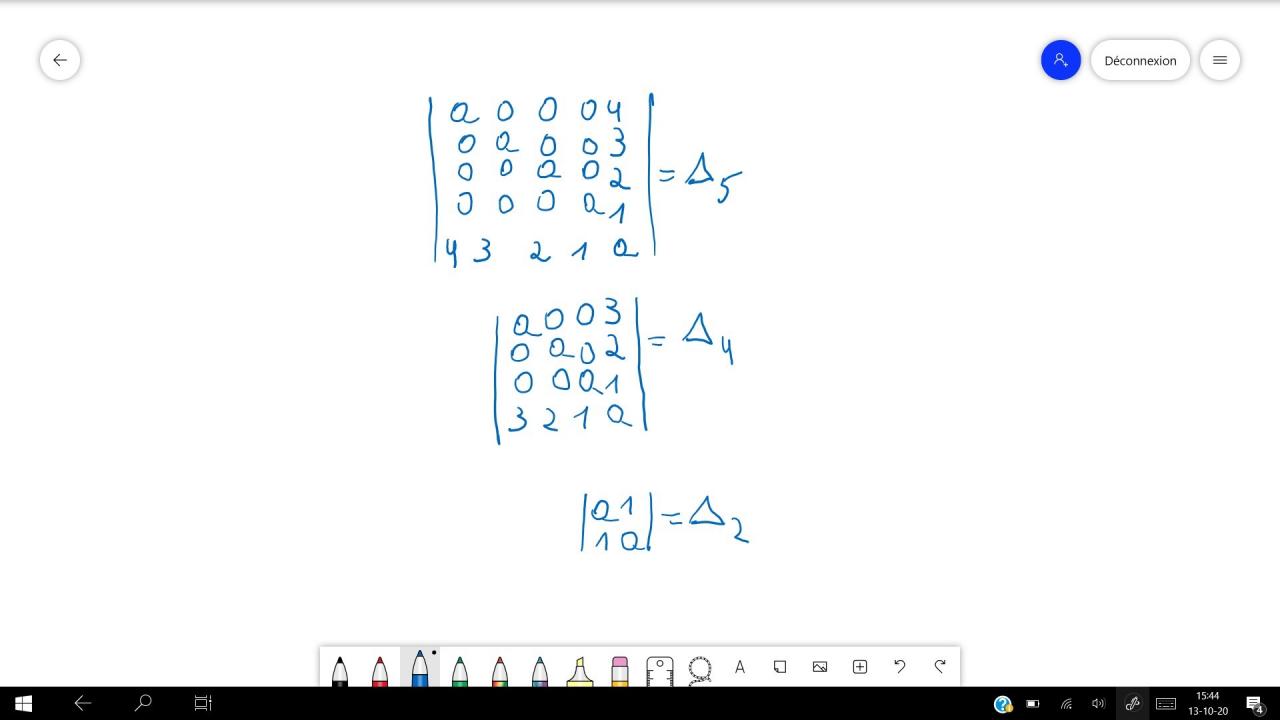
Bonjour, j'ai une question par rapport à un exercice de math qui me bloque complètement, on me donne pour tout n supérieur ou égal à 2 le déterminant delta n suivant où a est un réel.
|a 0 ... 0 n-1|
|0 a ... ... ...|
|... ... ... 0 2|
|0 ... 0 a 1|
|n-1 ... 2 1 a|
On me demande de calculer delta pour n = 2 et de montrer que pour tout n supérieur à 2, delta n vérifie une relation récurrente de ce type delta n = q( delta (n-1)) + f (n) où q et f(n) sont à déterminer.
Mon problème c'est que je suis pas sur de bien comprendre la formulation du déterminant, je vois bien qu'il est symétrique et que la nième ligne et la nième colonne contienne des factorielles de n-1 plus le terme a.
Mais pour la 1 ère question je ne sais pas si quand on me dit n = 2 je peux écrire ça | a 1| parce que factorielle de 1 contient juste 1 et qu'on rajoute le a ou bien si je dois uniquement
| 1 a|
remplacer le n et donc trouver une expression pour ce déterminant du genre a x delta 1 + (-1)^(i+j) (n-1) (-1)^(i+j) a^(n-2) si j'utilise la 1 ère ligne que je multiplie par les cofacteurs, et je ne sais même pas si la proposition que je viens d'écrire est correcte du coup ça me bloque pour le reste.
Est ce que certains d'entre vous savent m'aider? Merci d'avance
-----