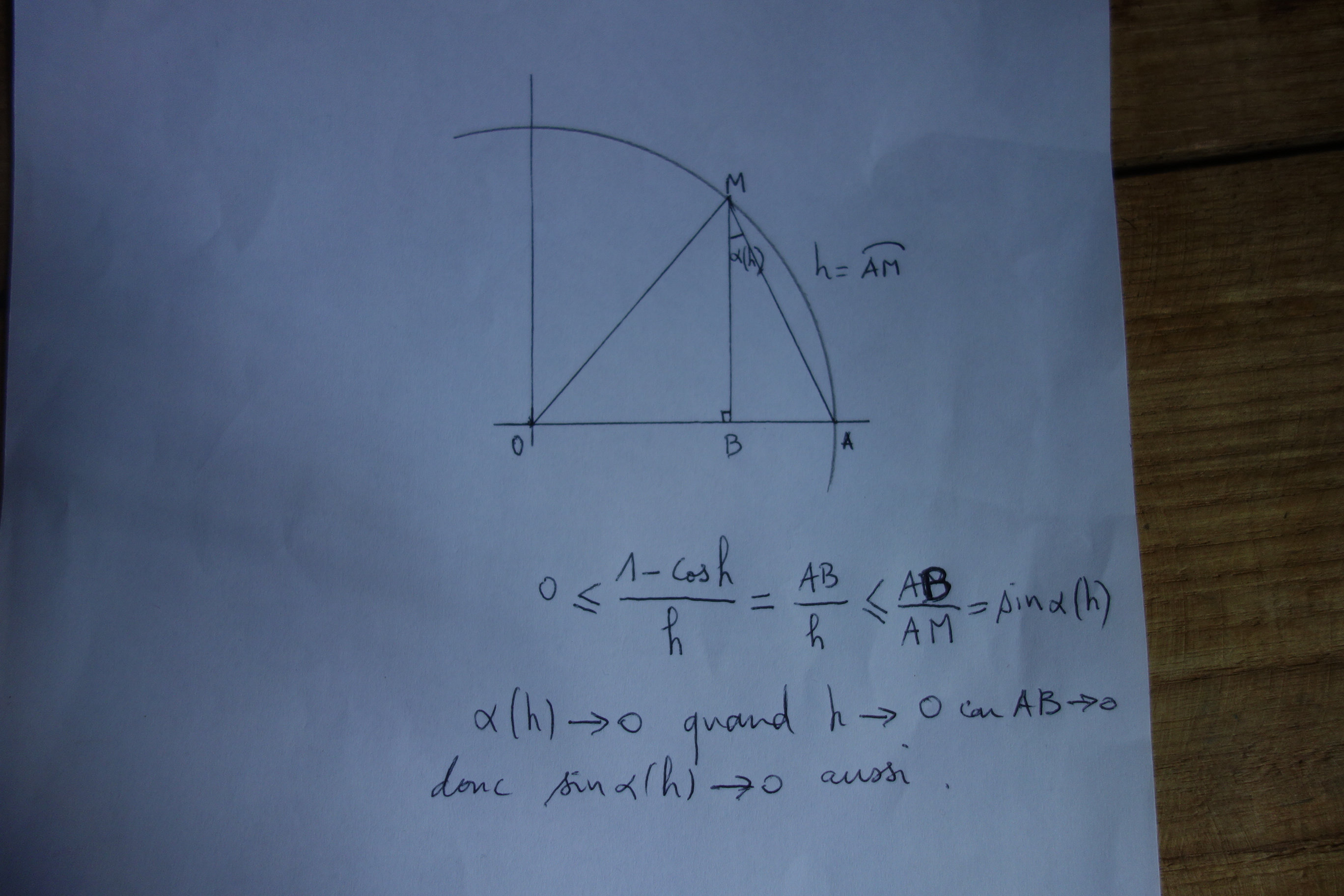
Le diable se cache dans les détails.
Et comme Stefjm a donné plusieurs discussions sur ce thème, qui exposent les détails et leurs diableries, tu peux voir ça facilement (au lieu de te contenter d'un "je ne doute pas".
Pour ma part, j'ai toujours vu des démonstrations de niveau 1ère S qui sautent ces détails, même ) l'époque où on faisait beaucoup de géométrie et des démonstrations géométriques assez "costaudes" au niveau première.
Cordialement
Par exemple pour (1-cosh)/h :
Oui,
c'est une très belle preuve intuitive, basée sur l'affirmation que l'arc de cercle est plus long que sa corde. Avec la notion intuitive (qui passe très bien en lycée, on l'utilise depuis des années sans justification) de longueur d'une courbe et l'affirmation mainte fois répétée "la ligne droite est le plus court chemin d'un point à un autre", ça passe tout seul.
Et tout ça est "vu sur la figure", comme toujours dans la géométrie élémentaire (et aussi celle d'Euclide). Et même tout au long des dix-septième et dix-huitième siècles.
On a commencé à s'en méfier au dix-neuvième, avec la découverte que des choses évidentes étaient sujettes à caution : continuité évidente des courbes, dérivabilité des fonctions continues, .. jusqu'à même la géométrie euclidienne (la seule possible selon Kant). Et on s'est mis, en mathématiques élaborées (*) à chercher des preuves plus sévères, plus rigoureuses.
Voilà pourquoi je n'ai pas proposé à Jall2 de construire les maths formalisées du supérieur à partir des mathématiques intuitives du secondaire, mais de retrouver ce qu'on disait en lycée comme conséquence des méthodes élaborées qu'on voit en supérieur.
Une bonne lecture : "Mathématiques, la fin des certitudes" par Morris Kline. Malheureusement plus édité, vendu d'occasion 60 € alors que neuf il en vaudrait 18.
Cordialement
(*) bien entendu, pas dans l'apprentissage des maths scolaires. La preuve que tu présentes est faite pour emporter la conviction des lycéens. Ceux qui feront des maths pour les maths apprendront à critiquer ce genre de présentation et à utiliser des outils plus convaincants.
Avec ce genre de preuve intuitive, j'arrive à montrer que 2=pi.
https://youtu.be/lD7zDnr6TBs?t=350
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Oulla les gars, soit il y a un malentendu depuis le depart entre nous, soit vous faites preuve d'une mauvaise foi sans limite !
Par prudence je suppose qu'il y a malentendu. Reprenons depuis le debut :
1) J'ai fait de la recherche en maths, je sais ce qu'est la rigueur et je la valorise en tant que tel bien entendu, mais ici n'oublions pas qu' il s'agit de fournir une preuve a notre primo posteur (etudiant en premiere annee de fac apparemment) que les developpements en serie entiere de sin et cos definis geometriquement a partir du cercle trigo sont bien ceux que l'on trouve a partir du developpement en serie de exp(it). Ici on est pas entre mathematiciens qui font de la recherche.
2) Le point faible de la definition geometrique des fonctions circulaires, c'est, on est tous d'accord, comment definir la notion de longueur d'un arc de cercle. On pourrait utiliser l'artifice de Bourbaki decrit plus haut (i.e. prouver l'existence de la fonction exp(it) sans passer par les series entieres) pour contourner le probleme, et cela donnerait une definition rigoureuse de la longueur d'un arc de cercle, ainsi que le fait qu'une corde est toujours plus petite qu'un arc. Et cela rendrait irreprochable la preuve que j'ai presente en deux morceaux plus haut.
3) Mais meme sans passer par l'existence de exp(it), on peut considerer comme plus que convaincante cette preuve "modulo" le flou sur la longueur de l'arc et sur le fait que la corde est plus petite que l'arc. Car ce sont des notions et des faits dont l'esprit ne peut douter. Et c'est malhonnete de le mettre sur le meme plan que la fausse demonstartion que 2=pi, car cela n'a rien a voir : on voit tout de suite le probleme avec cette fausse demonstration, meme sans passer par des notions telles que la longueur d'une figure fractale. Bien entendu dans ce cas on ne peut pas dire qu'il s'agit d'une demonstration totalement rigoureuse de 1), mais il ne faut pas confondre le fond et la forme en maths : le fond c'est l'essentiel, et la forme c'est l'habillage formel donne a ce fond. La forme est importante aussi bien sur, mais a mon avis le fond bien plus, autant pour un etudiant (meme de fac) que pour un chercheur (n'oublions pas que des gens comme Gauss, Riemann ou Poincare pour ne citer qu'eux, ne possedaient pas une rigueur telle qu'on la concoit aujourd'hui, mais ont eu des idees extremement fecondes qui sont allees au fond des choses). Ici on est sur le fond, avec une forme certes un peu bancale, mais pas tant que cela finalement. Et cela emporte la conviction du lecteur sans aucun doute possible.
Dernière modification par syborgg ; 15/11/2020 à 19h19.
PS: excusez moi pour les accents mais j'ai un clavier americain.
Voyons Syborgg,
la question initiale n'est pas ce que tu dis, mais "Comment montre-t-on l'équivalence des 2 définitions ?"
C'est toi qui t'enferres à vouloir à tout prix que ce qu'on fait en première en trigo soit des mathématiques rigoureuses.
Pour ma part, j'ai dit ce que j'avais à dire. Je ne poursuivrai pas ce faux débat.
Cordialement.
Si tu relis attentivement mon dernier post, tu verra que je n'ai pas pretendu que ce qu'on fait en premiere en trigo est rigoureux.
Et je ne vois pas la difference entre ce que je dis dans 1) du dernier post et l'equivalence entre les definitions des fonctions circulaires facon trigo et facon serie entiere.
Oh, je ne comprends pas grand chose en maths, mais j'ai vite fait d'en profiter...
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
