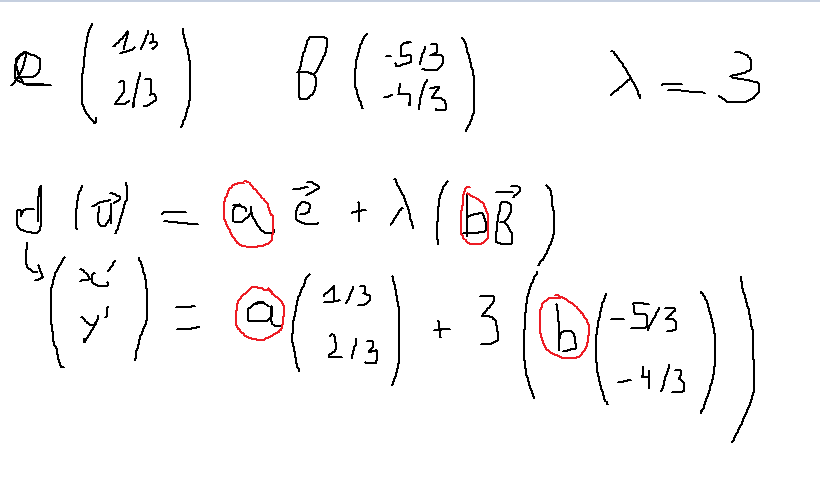Dilatation vecteur

[snsdtiti]

Bonjour,
Avec mon équipe de 4 cerveaux, on arrive pas à résoudre un problème TT

Soit un vecteur quelconque du plan u=(x,y). On note u'=(x',y') l'image de ce vecteur par la dilatation vectorielle de rapport 3 par rapport à la droite vectorielle D
(de vecteur directeur e=(1/3, 2/3) ), parallèlement à la droite vectorielle Delta (de vecteur directeur f=(-5/3, -4/3) .

On veut modéliser cette application linéaire sous la forme d'un produit matriciel: (le tout entre parenthèse mais j'y arrive pas ^^')
x'. = a c + x
y'. = b d. + y


on cherche a et b
on a la formule d(u) = ae +lamda*b*f mais on voit pas du tout du tout....

Merci
-----

[gg0]

Je ne connaissais pas les dilatations, mais après avoir vaguement regardé, je comprends que c'est mal parti pour vous !

Partons de la formule de votre cours, qui est ici très incomplète (ne jamais se contenter de la formule seule, toujours lire ce qui la précède ou la suit, et qui explique !!!)

Soit (*) où e dirige la droite et f la direction de dilatation. Alors

Vous, vous avez u = (x,y), donc il va vous falloir exprimer u dans la base (e,f), donc trouver le a et le b de la formule, puis en déduire u' en fonction de e et f, puis u' comme couple de réel. Et vous verrez apparaître la matrice, très exactement le produit de la matrice par le vecteur colonne (x,y)^t.

Cordialement.

(*) (e,f) est une base. C'est nécessaire pour avoir une dilatation.

[snsdtiti]

Merci pour votre réponse.

On a pas trouvé d'info sur internet et dans le cours on a juste la formule (mais vraiment y a rien d'expliqué...) et l'énoncé c'est exactement ce que je vous ai envoyé...
Du coup voila ce qu'on a fait :



et on sais pas comment trouver le a et le b...

Merci

[gg0]

Je vous ai donné les éléments pour faire votre travail. Faites ce que vous voulez.

[A voir en vidéo sur Futura]

[snsdtiti]

Merci pour la réponse mais ça nous aide pas du tout...
Je viens pour demander de l'aide, c'est pas comme si on n'y avait pas mis d'effort si c'est pour ne pas nous aider un peu ou juste un indice c'est pas la peine de répondre.

En tout cas si une âme charitable vient à notre secours nous lui en seront reconnaissant mais si c'est juste pour nous jeter ça comme ça c'est pas la peine.

Merci.

[gg0]

Tu viens demander de l'aide, mais tu la refuses.
Adresse-toi à ton prof pour avoir un cours clair sur ces notions, ce que tu dis de ton cours n'est pas sérieux, une formule sans explication de ses notations ça n'est pas une formule : Ce n'est pas des maths, seulement de la calligraphie.

Et ce n'est pas la première fois que tu viens demander une aide avec ces questions de géométrie pas très difficiles quand on a les bases d'algèbre linéaire et les définitions correctes. Je te donnes les définitions correctes, dans le message #2, tu me renvoies un document sans utilité ("voilà ce qu'on a fait"), sans utilité puisque vous ne savez pas qui sont a et b. Au lieu de bien regarder ce que je vous ai dit (la définition) et de vous en servir.

Je ne nie pas vos efforts, je vous reproche de les faire pour rien puisque vous n'avez pas copié sur le polycop la définition, seulement une formule magique. Et de ne pas les faire à partir de la bonne définition. de na pas avoir cherché à comprendre, dans votre polycop ce que sont ce a et ce b, et ne ne pas accepter le guidage que je vous proposais, qui les définit.

Et la charité n'a rien à faire ici, les règles du forum sont claires : On ne fera pas les exercices à votre place.

Cordialement.

[jacknicklaus]

mais si c'est juste pour nous jeter ça comme ça c'est pas la peine.

Alors là, tu exagères, gg0 t'as donné une démarche très claire et précise, mais tu ne la suis pas.

2ème chance :
Tu as deux vecteurs e et f qui forment une base. Appelons (i,j) la base d'origine
Soit u un vecteur de coordonnées (x,y) dans la base (i,j)

La définition de la dilatation exige de commencer par exprimer u dans la base (e,f). On nomme (a,b) les coordonnées de u dans cette base. On a donc u = a.e + b.f
Toujours dans cette base, la dilatation s'exprime simplement D(u) = a.e + lambda.b.f
le jeu consiste donc à exprimer u dans la base (e,f), c'est à dire calculer a et b en fonction de x et y, puis appliquer D sur u ce qui est très simple en base (e,f), puis revenir exprimer le résultat dans la base d'origine (i,j).

Commençons par le début :

On te donne e et f exprimés dans la base (i,j). Ils forment une base. soit u (x,y) un vecteur quelconque dans la base (i,j).
Je note U_i,j le vecteur colonne (x,y), qui est U exprimé en coordonnées dans la base (i,j) : u = x.i + y.j
Je note U_e,f le vecteur colonne (a,b), qui est U exprimé en coordonnées dans la base (e,f) : u = a.e + b.f

1) On a donc, sans calcul, U_i,j = M U_e,f où M est une matrice 2x2. Peux tu donner les coefficients de cette matrice (aucun calcul nécessaire)

2) En conséquence on peut écrire U_e,f = M^-1U_i,j. Peux tu calculer les coefficients de cette matrice M^-1 ?


Fais déjà celà, on verra pour la suite.