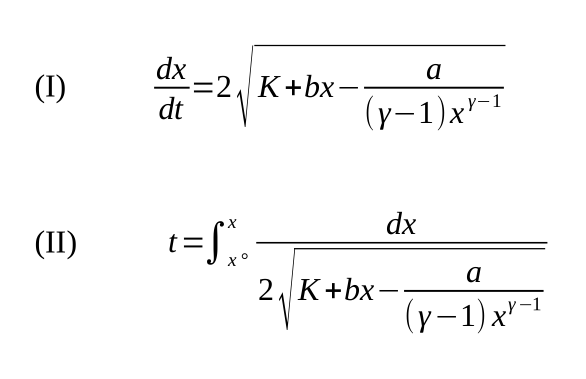Bonjour, dans le cadre d'un problème de dynamique je suis amené à résoudre une équation de la forme x'' = a*x^n + b
x'' est en fait une accélération, a une valeur réelle qui dépends des conditions initiales, n=-y = -1.4 le coefficient adiabatique de l'air et b est une constante tenant compte de la contribution de la pression atmosphérique.
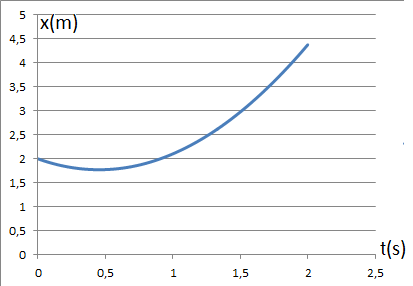
J'aimerais si possible avoir une équation de la forme x = f(t) équation horaire de la position.
Je n'ai pas trouvé de méthode usuelle pour résoudre une équation comme celle-ci sur internet.
Merci d'avance.
-----