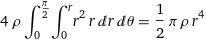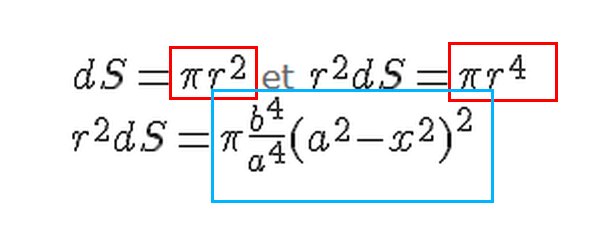Bonjour,
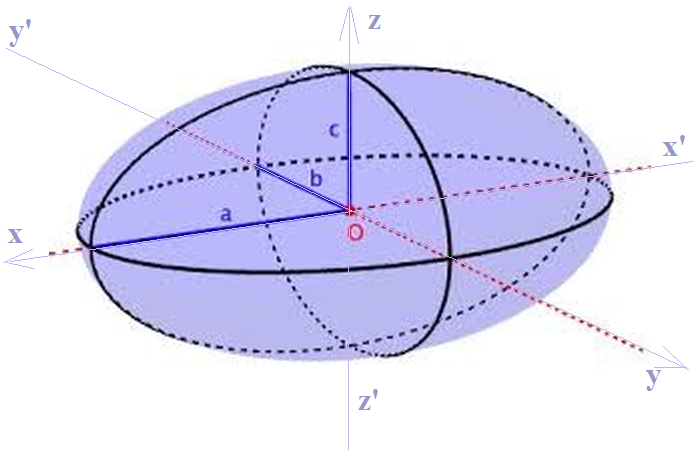
J'aimerais calculer le moment d'inertie Ixx d'un prolate sphéroïdal (ellipsoïde aplati) suivant l'axe de révolution x.
prolate.pngprolate2.jpg
I_xx=ρ_s ∬(y^2+z^2) dS
La question est comment je défini l'élément de surface pour mon intégrale ?
Pour mon ellipsoïde a>b et b=c.
Merci,
MCK
-----



 !(Ou Calculus III)
!(Ou Calculus III)