Rotations dans un ordre d'axe différent

[Minuitdixhuit]

Rotations dans un ordre d'axe différent

Bonjour, voici la problématique pour laquelle je sollicite votre aide.

J'ai 2 cubes rigoureusement identiques que je peux mouvoir en rotation selon 3 axes x, y et z orthonormés qui sont identiques pour les deux.

Cependant les rotations du premier cube se font obligatoirement dans l'ordre y, puis x, puis z.
Par exemple A1y, B1x, C1z

et les rotations du second cube obligatoirement dans l'ordre x, puis y, puis z.

Je voudrais connaître la «formule» qui me permettrait, connaissant A1y, B1x, C1z, de déterminer les valeurs A2x, B2y, C2z à appliquer au second cube dans son ordre propre afin qu'il se retrouve dans la même position.
Sans doute de la forme
A2x = f1(A1y, B1x, C1z)
B2y = f2(A1y, B1x, C1z)
C2z = f3(A1y, B1x, C1z)
Bien sûr je trouve les valeurs triviales quand les angles sont de 0º, 90º, 180º, -90º ou -180º mais je sèche sur les valeurs intermédiaires.

Je crains que la solution passe par un calcul matriciel... que je ne domine pas bien. Si une expression linéaire était possible se serait un rêve...
Merci pour votre aide.


-----

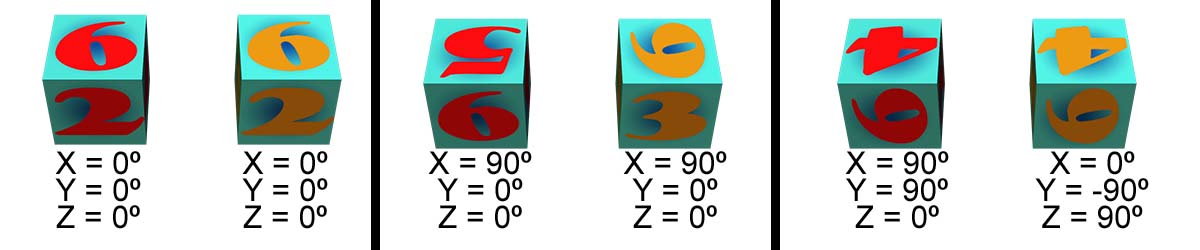
[Omega3.0]

Bonjour,
Cela me rappelle la cristallographie.
Pour un cube il y a 3 axes de rotation d'ordre 4: axe passant par le centre des faces opposées Rotation de 0, 90, 180, 270 °
et 3 axes de rotation d'ordre 3 : axes les 3 diagonales du cube Rotation de 0, 120, 240 °.
Les matrices 3*3 représentant les rotations sont simples car elles ne comportent que des sin, cos d'angles remarquables.
Le produit de plusieurs rotations est le produit des matrices (pas commutatif).
Sinon il y a les quaternions, sorte de complexe à 4 nombres réels qui sont liés aux rotations mais plus compliqués à manipuler.
Je ne pense pas qu'il existe une méthode pour trouver la fonction f(...) sauf à essayer toutes les combinaisons possibles des différentes rotations.
Par intuition 3 rotations doivent être suffisantes???

[GBZM]

Bonjour,

On peut effectivement faire les calculs à l'aide des quaternions, en utilisant les ressources du calcul formel. J'utilise le logiciel SageMath.
Pour la mise en équation, j'utilise la tangente de l'angle moitié de rotation ; ça a l'inconvénient d'oublier les demi-tours, mais aussi l'avantage de minimiser le nombre de variables et de permettre un traitement entièrement algébrique.

Je note a,b,c (resp. t,u,v) les tangentes des demi-angles de rotation pour les rotations d'axes x,y,z sur le premier (resp. deuxième) dé.

Le quaternion correspondant à la rotation du premier dé est (à un facteur réel non nul près) (1+c*k)*(1+a*i)*(1+b*j)), où (i,j,k) est la base de l'espace des quaternions purs, correspondant aux axes x,y,z.
Le quaternion correspondant à la rotation du deuxième dé est (toujours à un facteur réel non nul près) (1+v*k)*(1+u*j)*(1+t*i).

On écrit que ces deux quaternions sont égaux à un facteur réel près, et on trouve qu'étant donnés a,b,c il y a deux solutions pour t,u,v, avec

t solution de l'équation
a*(b^2 + 1)*t^2 + (a^2 - 1)*(b^2 - 1)*t - a*(b^2 +1)=0 .
On remarque que les deux solutions sont de produit -1, ce qui veut dire que les angles de rotation diffèrent de pi.

u donné par u = (t-a)/(b*(t + a)).

v donné par v = - ((a*b*c + 1)*t + b*c - a )/((a*b + c)*t - a*c - b)

Je donne mon code SageMath, mais il demande un peu de familiarité avec les manipulations sur les idéaux de polynômes.

R.<a,b,c,t,u,v>=PolynomialRing(QQ,6)
F=FractionField(R)
H.<i,j,k>=QuaternionAlgebra(F,-1,-1)

r=((1+c*k)*(1+a*i)*(1+b*j)).coefficient_tuple()
s=((1+v*k)*(1+u*j)*(1+t*i)).coefficient_tuple()

I=R.ideal([s[0]*r[i+1]-r[0]*s[i+1] for i in range(3)])
PD=I.primary_decomposition()
J=PD[-1]

S.<a,b,c,t,u,v>=PolynomialRing(QQ,6,order="invlex")
K=J.change_ring(S)
G=K.groebner_basis()
G

La dernière commande renvoie cette liste de polynômes, où l'on retrouve les résultats donnés plus haut (l'équation en t est le dernier polynôme de la liste) :

[c*u*v + a*b*u*v - b*c*v + a*v - a*b*c*u + u - a*c - b, c*t*v + a*b*t*v - a*c*v - b*v - a*b*c*t + t + b*c - a, a*b^2*t*v + a*t*v - 2*a*b*c*v - b^2*v + v - a*b^2*c*t - a*c*t + b^2*c - c - 2*a*b, a*b*c^2*v + 1/2*a^2*b^2*c*v + 1/2*b^2*c*v - 1/2*a^2*c*v - 1/2*c*v - a*b*v + 1/2*a*b^2*c^2*t + 1/2*a*c^2*t + 1/2*a*b^2*t + 1/2*a*t - 1/2*b^2*c^2 + 1/2*c^2 + 2*a*b*c + 1/2*a^2*b^2 - 1/2*a^2, b*t*u + a*b*u - t + a, a*t*u + u + a*b*t - b, a^2*b*u - b*u - a*b^2*t - a*t + b^2 + a^2, a*b^2*t^2 + a*t^2 + a^2*b^2*t - b^2*t - a^2*t + t - a*b^2 - a]

[Minuitdixhuit]

Merci beaucoup là.... Mais je suis complètement dépassé. Je me vois mal transcrire cela en Python, à la rigueur en Visual Basic, les seuls que je puisse utiliser pour interfacer avec mon application. Je vais essayer d'aborder le problème d'une autre façon.

[A voir en vidéo sur Futura]

[GBZM]

Tu peux parfaitement rentrer les résultats du calcul symbolique dans une procédure python.
Quelle que soit la façon dont tu abordes le problème, tu auras toujours le même résultat !

[Minuitdixhuit]

Merci.
En fait j'ai besoin de.... 6000 à 8000 calculs... sur des données qui me sont fournies par Python. Ensuite il me faut les exploiter et les réinjecter par Python. La bonne nouvelle, c'est que ce n'est pas nécessairement en temps réèl. Je ne suis pas encore certain de savoir le faire. Il me faut réfléchir encore...

[GBZM]

Une procédure python qui fait ce que tu veux (avec des angles exprimés en radians, tu préférerais peut-être en degrés, mais ça c'est facile à changer)

import numpy as np

def change_ordre(angle_y,angle_x,angle_z) :
    # angle_y, angle_x et angle_z sont les angles (en radians)
    # des rotations suivant les axes y, x et z
    # la procédure retourne les angles de rotation quand on les
    # effectue dans l'ordre x, y, z
    a = np.tan(angle_x/2)
    b = np.tan(angle_y/2)
    c = np.tan(angle_z/2)
    t = -1/2*((a**2 - 1)*(b**2 - 1) - 
              np.sqrt((a**2 - 1)**2*(b**2 - 1)**2 
                      + 4*a**2*(b**2 + 1)**2))/a/(b**2 + 1)
    u = -(a*b*t - b)/(a*t + 1)
    v = (b*c - (a*b*c - 1)*t - a)/(a*c - (a*b + c)*t + b)
    return 2*np.arctan(t), 2*np.arctan(u), 2*np.arctan(v)

J'ai même vérifié que ça marchait bien. Pour cela, je fais une procédure de calcul de matrice de rotation :

def mat_rot(axe,angle) :
    if axe == 'x' : i=0
    elif axe == 'y' : i=1
    elif axe == 'z' : i=2
    mat = np.zeros((3,3))
    mat[i,i] = 1
    c = np.cos(angle) ; s=np.sin(angle)
    j=(i+1)%3 ; k=(i+2)%3
    mat[j,j] = c ; mat[k,k] = c
    mat[k,j] = s ; mat[j,k] = -s
    return mat

et je vérifie sur un exemple :

ay,ax,az = .5, .4, .3
bx,by,bz = change_ordre(ay,ax,az)
mat1=np.matmul(mat_rot('z',az), np.matmul(mat_rot('x',ax), mat_rot('y',ay)))
mat2=np.matmul(mat_rot('z',bz), np.matmul(mat_rot('y',by), mat_rot('x',bx)))

print(bx,by,bz)
print(mat1)
print(mat2)

J'ai les nouveaux angles, et la rotation est bien la même :

0.44895778584603324 0.45735908504957035 0.5096152133834368
[[ 0.78321388 -0.27219214  0.55900578]
 [ 0.43770193  0.87992318 -0.1848032 ]
 [-0.44158016  0.38941834  0.80830707]]
[[ 0.78321388 -0.27219214  0.55900578]
 [ 0.43770193  0.87992318 -0.1848032 ]
 [-0.44158016  0.38941834  0.80830707]]

[Minuitdixhuit]

J'en suis baba....
Bon, tu n'as pas eu la politesse de me laisser le temps de réfléchir, mais je ne vais pas t'en vouloir...
Je vais mettre ça en oeuvre dès que possible et je te recontacte pour te monter le merveilleux résultat de ta baguette magique.
Merci encore.

Miguel

[GBZM]

Une chose m'étonne. Pourrais-tu expliquer pourquoi tu as besoin de faire cela et pourquoi tu as 6000 ou 8000 calculs à faire ?

[Minuitdixhuit]

C'est vrai, j'aurai pu en parler...
Bon en gros je fais de l'animation 3D. Des petits clips video genre dessin animé pour des chanteurs. Donc j'ai écrit en VB et en Python toute une série de programmes qui créent des fichiers d'animations pour divers instruments de musique y compris la bouche. L’intérêt est que mes programmes peuvent lire des partitions au format XML musical (un des standards de fichiers musicaux) et les transforment directement en fichier type FBX (un des standards de fichiers d'animation).
Bien...
Mes personnages animés ont un corps que je peux mouvoir en rotation et en translation.
A ce corps sont attachés les hanches auxquelles sont attachés l'abdomen, les cuisses etc....
Bien...
Je récupère à droite et à gauche des fichiers d'animation tout fait, par exemple des danses. Malheureusement ces fichier pour positionner et animer le personnage dans l'espace utilise parfois le corps, parfois les hanches...
Et moi je veux que le corps définisse une position statique dans l'espace, par exemple sur une estrade et les hanches les «tortillements» de, par exemple une danse.
Malheureusement, le noeud du problème est que les rotations ne se font pas dans le même ordre... D'où ma requête... et comme un clip peut faire plus de 10000 images...
Voilà une exemple d'une de mes réalisations.

https://youtu.be/QmItNElWZtM

[GBZM]

Merci, c'est intéressant.

Une autre question que je me pose souvent :
Souvent je vois des gens décomposer les rotations spatiales en rotations suivant les 3 axes, comme ici y-x-z et x-y-z. Je me demande pourquoi les angles d'Euler ne sont pas plus souvent utilisés. Ils correspondent à une décomposition z-x-z.

[Minuitdixhuit]

Pour l'ordre choisi je ne saurais pas te répondre. On trouve chez le même fabricant des ordres différents pour des personnages humanoïdes qui se ressemblent pourtant... Sans doute que les développeurs informaticiens n'ont pas saisi l'importance du problème inter-plateforme. Et je ne te parle pas de l'unité de déplacement qui vaut 1m pour certains, 1 km pour d'autres et un pied ou un pouce. Mais là le problème est facile à résoudre.
La 3D est une discipline semi-artistique ou l'on croise des informaticiens auto proclamés (comme moi), des créateurs qui bidouillent des scripts et se fiche de sa robustesse et pas beaucoup de mathématiciens...

[Minuitdixhuit]

Je reviens à nouveau sur le problème, tardivement car je ne me souvenais plus du site où j'avais posté ma question... Mes excuses.
J'ai essayé la solution proposée mais j'obtiens des résultats aberrants mais je ne sais pas où se trouve mon erreur :

import math

import numpy as np

def change_ordre(angle_y,angle_x,angle_z) :
    # angle_y, angle_x et angle_z sont les angles (en radians)
    # des rotations suivant les axes y, x et z
    # la procedure retourne les angles de rotation quand on les
    # effectue dans l'ordre x, y, z
    a = np.tan(angle_x/2)
    b = np.tan(angle_y/2)
    c = np.tan(angle_z/2)
    t = -1/2*((a**2 - 1)*(b**2 - 1) - 
              np.sqrt((a**2 - 1)**2*(b**2 - 1)**2 
                      + 4*a**2*(b**2 + 1)**2))/a/(b**2 + 1)
    u = -(a*b*t - b)/(a*t + 1)
    v = (b*c - (a*b*c - 1)*t - a)/(a*c - (a*b + c)*t + b)
    return 2*np.arctan(t), 2*np.arctan(u), 2*np.arctan(v)


def cube(degY, degX, degZ) :
	Yrad = math.radians(degY)
	Xrad = math.radians(degX)
	Zrad = math.radians(degZ)

	print "degY " + str(degY)
	print "degX " + str(degX)
	print "degZ " + str(degZ)
	print " "
	
	
	A, B, C = change_ordre(Yrad, Xrad, Zrad)

	degA = math.degrees(A)
	degB = math.degrees(B)		
	degC = math.degrees(C)
	
	print "degA " + str(degA)
	print "degB " + str(degB)	
	print "degC " + str(degC)
	print "***********************"

cube(0, 0, 0)
cube(30, 30, 30)
cube(90, 0, 0)
cube(90, 90, 0)

Et j'obtiens les résultats suivants :

degY 0
degX 0
degZ 0

degA nan
degB nan
degC nan
***********************
degY 30
degX 30
degZ 30

degA 62.3941098803
degB 21.8624678481
degC 142.759911836
***********************
degY 90
degX 0
degZ 0

degA nan
degB nan
degC nan
***********************
degY 90
degX 90
degZ 0

degA 126.869897646
degB -36.8698976458
degC -90.0

En particulier dans ce cas j'attendais quelque chose comme
x = 90
y = 0
z = 90
***********************

Merci pour votre aide.

[GBZM]

Depuis le temps ! Il a fallu que je fouille dans mes archives pour retrouver le notebook python.

J'ai modifié pour travailler en degrés et tenir compte des exceptions qui provoquent les "NAN", mais je n'ai rien changé aux formules :

def change_ordre_deg(angle_y,angle_x,angle_z) :
    # angle_y, angle_x et angle_z sont les angles (en degrés)
    # des rotations suivant les axes y, x et z
    # la procédure retourne les angles de rotation quand on les
    # effectue dans l'ordre x, y, z
    a = np.tan(np.radians(angle_x/2))
    b = np.tan(np.radians(angle_y/2))
    c = np.tan(np.radians(angle_z/2))
    if b==0 : t=a; u=0; v=c
    elif a==0 : t=0; u=b; v=c
    elif a!= 0 :
        t = -1/2*((a**2 - 1)*(b**2 - 1) - 
              np.sqrt((a**2 - 1)**2*(b**2 - 1)**2 
                      + 4*a**2*(b**2 + 1)**2))/a/(b**2 + 1)
        u = -(a*b*t - b)/(a*t + 1)
        v = (b*c - (a*b*c - 1)*t - a)/(a*c - (a*b + c)*t + b)
    return round(np.degrees(2*np.arctan(t)),2),\
round(np.degrees(2*np.arctan(u)),2),round(np.degrees(2*np.arctan(v)),2)

[GBZM]

Et tout va bien :

for data in [(0,0,0), (30,30,30),(90,0,0),(90,90,0)] : 
    print(change_ordre_deg(data[0],data[1],data[2]))

(0.0, 0.0, 0.0)
(33.69, 25.66, 46.1)
(0.0, 90.0, 0.0)
(90.0, 0.0, 90.0)

[Minuitdixhuit]

Merci beaucoup !
Je confirme que les valeurs que vous obtenez donne un bon résultat !
MAIS
Mon code ne donne pas les mêmes valeurs que le votre alors que c'est un simple copier-coller !!!
Je précise que je suis sous python 2.x. car mon application ne reconnait que celle là (Python for Poser 3D)
Est-ce que cela pourrait en être la cause ?????
J'ai juste supprimé les commentaires à cause des accentués qui ne sont pas reconnus par Python 2.x

import numpy as np


def change_ordre_deg(angle_y,angle_x,angle_z) :
    a = np.tan(np.radians(angle_x/2))
    b = np.tan(np.radians(angle_y/2))
    c = np.tan(np.radians(angle_z/2))
    if b==0 : t=a; u=0; v=c
    elif a==0 : t=0; u=b; v=c
    elif a!= 0 :
        t = -1/2*((a**2 - 1)*(b**2 - 1) - 
              np.sqrt((a**2 - 1)**2*(b**2 - 1)**2 
                      + 4*a**2*(b**2 + 1)**2))/a/(b**2 + 1)
        u = -(a*b*t - b)/(a*t + 1)
        v = (b*c - (a*b*c - 1)*t - a)/(a*c - (a*b + c)*t + b)
    return round(np.degrees(2*np.arctan(t)),2),\
round(np.degrees(2*np.arctan(u)),2),round(np.degrees(2*np.arctan(v)),2)


for data in [(0,0,0), (30,30,30),(90,0,0),(90,90,0)] : 
    print(change_ordre_deg(data[0],data[1],data[2]))

Résultat :

(0.0, 0.0, 0.0)
(62.39, 21.86, 142.76)
(0.0, 90.0, 0.0)
(126.87, -36.87, -90.0)


Qu'en pensez-vous ?

[GBZM]

C'est la mauvaise blague de python2 qui retourne -1 quand on rentre -1/2. J'arrive aux même résultats que toi sous python3 quand je remplace le -1/2 de la formule par -1//2 (quotient dans la division euclidienne des entiers).
Pour contourner ça, remplace dans la formule le -1/2 par 0.5, et normalement tout va rentyrer dans l'ordre.

[GBZM]

Remplacer -1/2 par -0.5, voulais-je dire.

[Minuitdixhuit]

Super !!!!!!!!!!!!!!!!!!!!!!!! Ça marche !!!
Bon je reste sur mon avis concernant la programmation Python...
Mais le plaisir est que tu m'ais donné la solution mathématique !!!
Je vais gagner un temps fou.
Encore merci !

[Minuitdixhuit]

Le premiers essais sont concluants.
Comme je m'en doutais un peu ça "bugue" aux limites par exemple 360, 360, 360 donne un résultat 0, 0, -90 mais ça n'a pas trop de conséquences. Il doit y a avoir d'autres curiosités aux alentours des gimbals locks.
J'ai eu besoin aussi de modifier le résultat du z, en lui ajoutant 360 si il était négatif au final, pour éviter un saut brusque de +180 à -180 mais cela ne remet pas en cause la formule.
Rien de gênant, ce n'est pas pour piloter une missile nucléaire que j'utilise ces belles formules, mais pour faire danser mes animations 3D.
Donc tout va bien.

[GBZM]

Tu peux régler le problème du 360 en remplaçant le if b==0 par if angle_y%360 ==0 et idem pour elif a==0 remplacé par elif angle_x%360==0.
Je ne comprends pas bien le problème du saut de +180° à -180° : comme c'est le même angle, où est le saut ?

[Minuitdixhuit]

Merci pour la première suggestion, je vais la tester aujourd'hui.
Pour le saut 180º -180º il faut examiner ça sous l'angle «physique» et non sous l'angle «math».
Dans un processus physique, un changement de phase, de direction, de masse etc... ne peut se faire instantanément, ne serait que pour des raisons d'inertie, d'énergie cinétique etc... Donc cela peut poser problème pour gérer ce changement pendant le transitoire.
Pour éclairer, dans mon cas précis, pour un film, j'ai des images par seconde. Si ce changement de phase s'effectue entre 2 images pas de problème on ne voit rien. Mais si je trouve le mouvement global trop rapide je vais «étirer» le temps en augmentant le nombre d'images entre l'image initiale inchangée et la finale inchangée. Ainsi le changement de phase peut s'effectuer sur une image et au lieu d'avoir 180 -180 invisible, l'objet est immobile dans la même position, j'ai par exemple 180 0 -180 et pendant une image l'objet n'est plus immobile.
La solution n'est plus automatique à ce moment là et demande, soit de ne pas s'approcher de ces angles durant la conception du mouvement, soit de gérer manuellement ce saut ensuite et cela est plus ou moins facile, mais pas automatique.
Dans le cas d'un missile nucléaire... c'est beaucoup plus problématique...
Je crois (sans certitude) qu'une fusée Ariane avait explosé il y a longtemps pour des raisons de cet ordre : l'adaptation de modèles ou de méthodes mathématiques à des processus physiques réels.
Excuse-moi d'être pédant ou un peu taquin, mais je dis souvent que les Mathématiciens sont des artistes très imaginatifs qui se permettent d'inventer des notions comme l'infini ou la racine de -1 et même le zéro (pas le zéro de numération, mais celui représentatif du «néant»), concepts extrêmement pratiques pour approcher de très près les phénomènes physiques, mais de très près seulement, pas de les décrire avec une «infinie» précision, puisque (vraisemblablement ?) le monde réel est de dimension continue et infinie donc non résolvable...

[GBZM]

Pas très convaincu par ton laïus, et encore moins par ta résolution du problème : "aussi de modifier le résultat du z, en lui ajoutant 360 si il était négatif au final". Tu élimines donc des sauts de 180 à -180 en rajoutant des sauts de 0 à 360.
Les angles pour les calculs de coordonnées n'interviennent que par leur cosinus ou leur sinus. Si tu as besoin d'interpoler, il vaut évidemment mieux le faire sur ces quantités, il n'y aura pas de saut causé par la détermination de l'angle.

[gg0]

L'échec du premier vol d'Ariane 5 est dû à un problème informatique. C'est lié à l'assiette de la fusée (l'angle avec la direction prévue), mais pas à un passage de 180° à -180° : La réutilisation d'un ancien programme avec un registre d'un octet de -127 à 128 avec des données sur deux octets a fait qu'à un moment les rectifications ont été inversée et l'angle a été accentué au lieu d'être corrigé, puis les corrections sont devenues erratiques et la trajectoire avec.

Cordialement.

[stefjm]

L'échec du premier vol d'Ariane 5 est dû à un problème informatique. C'est lié à l'assiette de la fusée (l'angle avec la direction prévue), mais pas à un passage de 180° à -180° : La réutilisation d'un ancien programme avec un registre d'un octet de -127 à 128 avec des données sur deux octets a fait qu'à un moment les rectifications ont été inversée et l'angle a été accentué au lieu d'être corrigé, puis les corrections sont devenues erratiques et la trajectoire avec.

Le bit de signe est particulièrement important pour les asservissements. Il est passé de numéro 7 à 15 sans crier gare...

[Minuitdixhuit]

Je suis d'accord. J'ai juste donné Ariane en exemple. Ce que je voulais exprimer c'est que la «modélisation» pouvait avoir des failles et là c'est bien le cas puisqu'elle n'avait pas envisagé des valeurs dans la gamme réelle des phénomènes physiques en les sous-estimant.

Pour ce qui et de :
"aussi de modifier le résultat du z, en lui ajoutant 360 si il était négatif au final" Tu élimines donc des sauts de 180 à -180 en rajoutant des sauts de 0 à 360."
c'est juste une solution qui fonctionne et non une règle justifiée. De plus il faut gérer en fait non pas les valeurs absolues négatives ou pas mais les variations de valeurs entre 2 images sinon on peut créer effectivement d'autres sauts aberrants.
Je précise cependant que dans la suite obtenue 178, 179, 180, -180, -179... si on ajoute 360 aux valeur négatives on obtient 178, 179, 180, 180, 179 et non un saut de 360. Ainsi il n'y a pas d'images intermédiaires dans des positions aberrantes.
Ce n'est encore une fois pas une règle ou une démonstration, mais du bidouillage.
J'ai donc appliqué la formule modifiée (sans ma pseudo règle des z négatifs) sur la séquence suivante :
Un cube d'ordre de rotation y, x, z, originellement en 0, 0, 0 prend linéairement la valeur 360, 360, 360 au bout de 360 images.
Ses coordonnées sont transmises via la formule modifiée à un cube d'ordre de rotation x, y , z. On obtient les courbes suivantes selon chacun de axes, le décrochement (180 -180) de la rotation z se situe à l'image 90 :
Cependant la rotation dans ce cas est parfaitement «visuellement» synchrone puisqu'il n'y a pas d'image entre l'image 90 et 91

X
Pièce jointe 466932
Y
Pièce jointe 466933
Z

[GBZM]

"Je précise cependant que dans la suite obtenue 178, 179, 180, -180, -179... si on ajoute 360 aux valeur négatives on obtient 178, 179, 180, 180, 179 et non un saut de 360. "
Et si tu ajoutes 360 aux valeurs négatives, alors la suite 2,1,0,-1,-2 te donnera 2,1,0,359,358 ! Tu élimines le changement de détermination pour un angle plat, tu le retrouves pour un angle nul. C'est inévitable, il n'y a pas de détermination continue de la mesure d'un angle.
Par contre, comme je l'ai déjà écrit, les fonctions cos et sin sont bien continues et si on veut interpoler entre deux angles, c'est bien entendu sur ces fonctions là qu'il faut interpoler et pas sur la mesure de l'angle. Je répète aussi que pour le calcul des coordonnées après rotation, un angle intervient toujours à travers les fonctions cos et sin.

[Minuitdixhuit]

Ok merci pour ton aide.