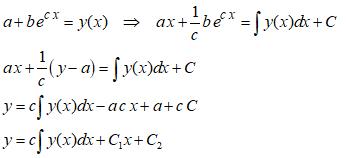Approximation d'une loi de refroidissement

[Tartozoeufs]

Bonjour,
Problème de math (ou de thermo) :

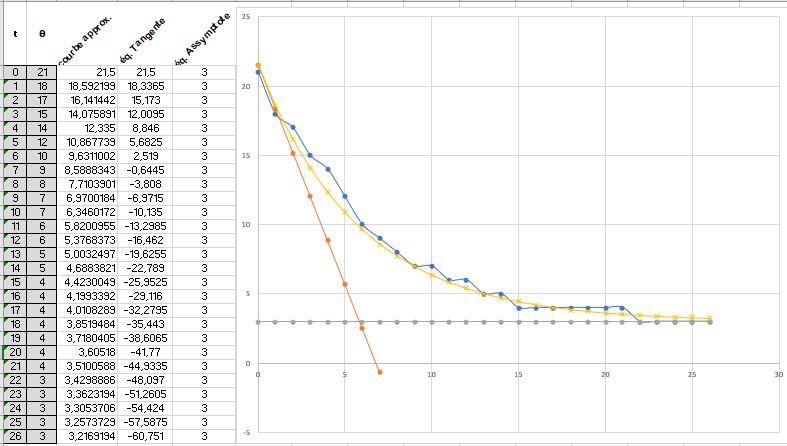
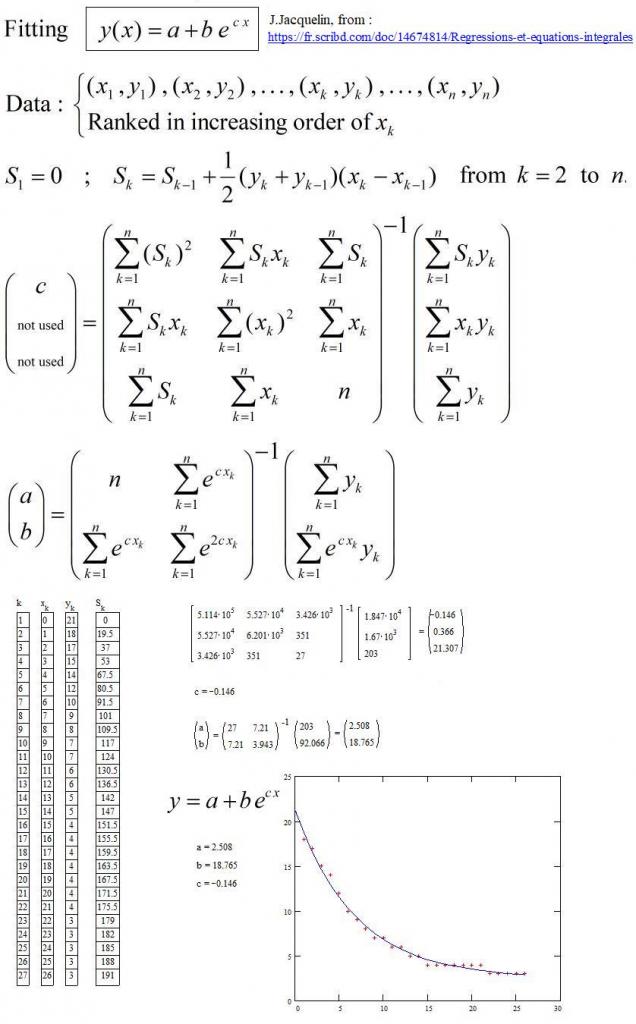
A température ambiante, on plonge un récipient fermé en plastique transparent (pour ne pas citer de marque), contenant un thermomètre, dans un bain d’eau et glaçons. On relève la température thêta(t) toutes les minutes. La température chute de 21°C à 3°C. Je sais que la loi de refroidissement est de la forme : thêta(t) = A. exp(-B.t) + C, c’est une donnée. Il faut trouver A, B et C.

Ce qui m’emm..bête c’est le C :
J’ai pensé utiliser les courbes de tendance Excel, mais l’équation ne comporte pas ce terme constant.
J’ai pensé passer en log népérien, je passe le C dans l’autre membre : ln(thêta – C) = ln(A) – B.t
mais thêta(t)-C < 0, log non défini.

Je pense que ce n’est pas un problème extraordinaire, c’est une classique loi de refroidissement et il doit y avoir une méthode pour le traiter. Est-ce que quelqu’un sait faire ? D’avance merci de vos bons conseils.
-----

[gg0]

Bonjour.

Le C est la température "à l'infini", la température d'équilibre au bout d'un temps infini; Donc tu le connais, c'est la température de l'eau avec des glaçons, au cas où on rajouterait autant de glaçons que nécessaire pour qu'il en reste toujours. C'est la température de fusion de la glace.
Ce n'est d'ailleurs pas une question de maths.

Cordialement.

[Tryss2]

, donc si tu as calculé A, et que tu connais ...

[gg0]

Autre remarque :

La température diminue, et thêta(t)-C = A. exp(-B.t) >0, et non pas <0. Le ln est bien défini.

[A voir en vidéo sur Futura]

[Tartozoeufs]

Merci gg0,
Je voyais plutôt ça comme un problème d’interpolation mathématique.
A priori on ne rajoute pas de glaçon, la température du bain est supposée constante pendant la manip. , j’imagine fonction de la masse d’eau et de la masse de glace, en assez grande quantité pour qu’elle ne varie pas significativement, de l’ordre de 3°C.
Merci Tryss2, J’ai avancé, je sais qu’à t=0, thêta(0) = A + C = 21°C, et d’une équation…
l’ordre de grandeur de A est entre 0 et 1 donc, A vaut environ 20°C,comme j’ai un point thêta(t) à 18°C, 18-20 <0 et ln(-2) n’est pas défini…

[gg0]

Il est évident qu'on ne va pas faire l'expérimentation un temps infini, mais la température du bain à 3° est plutôt celle du récipient à la fin de l'expérimentation, pas celle de l'eau avec des glaçons, qui est connue !!

Et tu continues à faire des calculs sans intérêt : "18-20 <0 et ln(-2) n’est pas défini… "

Mais si tu ne veux pas faire de la thermo dans un problème de thermo, c'est ton choix !!

[albanxiii]

On n'avancera pas plus tant qu'on n'aura pas les données, c'est à dire les résultats de mesure, la température et le temps associé.

[Tartozoeufs]

Merci albanxiii,
Rectificatif:
Merci gg0,
Je voyais plutôt ça comme un problème d’interpolation mathématique.
A priori on ne rajoute pas de glaçon, la température du bain est supposée constante pendant la manip. , j’imagine fonction de la masse d’eau et de la masse de glace, en assez grande quantité pour qu’elle ne varie pas significativement, de l’ordre de 3°C.
Merci Tryss2, J’ai avancé, je sais qu’à t=0, thêta(0) = A + C = 21°C, et d’une équation…
l’ordre de grandeur de A est entre 0 et 1 donc, C vaut environ 20°C,comme j’ai un point thêta(t) à 18°C, 18-20 <0 et ln(-2) n’est pas défini…
Les valeurs t en min:
t thêta(t)
0 21
1 18
2 17
3 15
4 14
5 12
6 10
7 9
8 8
9 7
10 7
11 6
12 6
13 5
14 5
15 4
16 4
17 4
18 4
19 4
20 4
21 4
22 3
23 3
24 3
25 3
26 3

[Tryss2]

Si on pose et

Alors calculer permet de trouver la valeur de , ce qui, en remplaçant par sa valeur dans l'expression de permet de trouver la valeur de A, et ainsi celle de C

[Tartozoeufs]

Pas trop rompu à l'utilisation du tr txt du site. Ci-joint une image des relevés sur excel avec une courbe de tendance Excel (qui ne colle pas du tout sans le terme constant).
Merci Tryss2, je pense que tu as raison,intuitivement je crois qu'il faut se débarrasser de cette constante C, dans un premier temps,trouver A et B. Je vas creuser ton idée on doit y arriver en calculant les deltas successifs et en trouvant une approximation par les moindres carrés sur Excel.
Je me disais peut être qu'en passant par la dérivé, on se débarrasse aussi de ce terme constant ?...je vais creuser.
En fait je suis nul en thermo, j'ai 55 ans ,age de l’équarrissage selon certains, si j'ai eu peut être été bon c'était il y a 30 ans, j'essaie d"aider mon fils, qui après les conditions d'étude en fac liées au contexte sanitaire, essaie de se créer un avenir...et puis on va quand même pas se laisser bouffer par les chinois !

[Tartozoeufs]

Données mesurés.

[Tartozoeufs]

Ci-avant les données + courbe de ces données en bleu + tangente à t=0 en orange obtenue en dérivant l'équation de la courbe jaune + asymptote y=3 en gris. La courbe jaune a été obtenue en "bricolant" les paramètres A,B et C sur une courbe d'équation thêta(t) = A. exp(-B.t) + C, pour coller au plus prés des relevées, équation thêta(t)=18,5.exp(-0,171.x)+3
Pièce jointe 436943
J'ai rien contre les chinois mais ils sont en train de nous bouffer quand même...

[RomVi]

Bonjour

La température d'un objet qui se refroidit suit une loi de type : t°finale + (t° initiale - t°finale)*e^(-t/tau)
On peut régresser tau avec le solveur de excel, ou sinon on le fait pour une ou plusieurs valeurs en calculant t/-ln(1-% de refroidissement)
le % de refroidissement correspondant à : (t° initiale - t° effective) / (t° initiale - t° finale)

[gg0]

A voir les données, la température finale de l'eau ne semble pas être celle de l'eau mélangée à des glaçons (température de fusion de la glace, par convention 0°C). Il y a sans doute peu à peu équilibre thermique entre le récipient et l'eau (*). La température "à l'infini" est aux alentours de 3°C, ce qui te donne une approximation de C (au choix, par excès 3, par défaut 2).
Dans sa réponse, ton fils a tout intérêt à ne pas se contenter d'arguments mathématiques (la courbe s'ajuste bien), mais de donner des arguments physiques, comme j'ai essayé d'en fournir. Et de justifier ses réponses par son cours.

Cordialement.

NB : la formule de RomVi correspond à une situation où l'environnement de l'objet est à température constante. Dans l'expérimentation, ce n'est pas le cas.
(*) il est possible aussi que la mauvaise conduction du plastique joue un rôle.

[RomVi]

La température "à l'infini" est aux alentours de 3°C, ce qui te donne une approximation de C (au choix, par excès 3, par défaut 2).

Attention, il y a une donnée dont tu n'as pas tenu compte : Les valeurs sont arrondies, donc à +/- 0.5°C près. On voit que la température fait un palier à 4, puis à 3, mais il n'y a pas assez de point pour dire si ça va continuer à baisser ou non.

Par ailleurs un autre phénomène est à prendre en compte : Aux alentours de 4°C il n'y a plus de convection naturelle, car la densité de l'eau remonte légèrement jusqu'à 0°C. Le transfert thermique s'effectue alors par pure conduction, et devient beaucoup plus lent. Une loi du 1er ordre ne va donc plus coller dans cette plage.

[gg0]

Oui, effectivement, j'en avais tenu compte pour proposer 2. Mais il est vrai que le modèle ne convenant plus, on peut en rester à C=0 en ne modélisant que la période d'expérience.

Cordialement.

[JJacquelin]

Une méthode très simple pour évaluer les trois paramètres de la fonction souhaitée de type exponentielle.
Pour la théorie concernant cette méthode, voir :
https://fr.scribd.com/doc/14674814/R...ons-integrales

[Tartozoeufs]

Je remercie toutes les bonnes volontés qui font travailler leurs neurones sur ce sujet, en espérant qu’il serve à d’autres.
Concernant la précision des mesures, je voudrais remercier M. Reverdy (https://www.youtube.com/channel/UCit...lLOktRwAhxMh8g), qui essaie d’enseigner une matière scientifique avec la difficulté de faire de l'expérimentation en distanciel et, en science, l’expérimentation, c’est indispensable. Il à envoyé à ses élèves une vidéo de l’expérience, faite avec « les moyens du bord » : filmé au smartphone, thermomètre à alcool…et cet exercice était à faire en petit groupe, pour créer du lien entre étudiant. MERCI.

[Tartozoeufs]

J’ai suivi les propositions de Tryss2 : en posant Capture d’écran 2021-04-16 120046.png
On se débarrasse ainsi des termes A et C, et j’arrive à Capture d’écran 2021-04-16 120157.png
exp(-B) se met en facteur et se simplifie ce qui ne mène à rien.
En calculant l’équation de la tangente en thêta 0, j’obtiens l’équation de droite Capture d’écran 2021-04-16 120346.png.
Ce qui ferait une équation de plus en récupérant graphiquement la droite tangente avec assez de précision.

[Tartozoeufs]

Merci RomVi et gg0, si je résume bien:
Capture d’écran 2021-04-16 122530.png

je sais maintenant que:
Capture d’écran 2021-04-16 122632.png

[Tartozoeufs]

Merci JJacquelin, je vous promets d'essayer de comprendre votre méthode "simple". je m'y atèle de suite.

[JJacquelin]

@ Tartozoeufs :

Je n'en demande pas tant ! Il serait plus intéressant de commencer par appliquer cette méthode afin de vérifier si elle convient et est suffisante dans votre cas concret. Vos observations et commentaires sur l'usage de cette méthode pourraient être utile à d'autres utilisateurs éventuels.

Ensuite, bien sûr, la démarche normale serait d'étudier la méthode afin de comprendre ses avantages et inconvénients et de pouvoir l'appliquer à bon escient dans d'autres cas et pour des fonctions différentes. En fait, son principe général n'a rien d'extraordinaire ni de génial et ne demande même pas de connaissances mathématiques avancées.

[Tartozoeufs]

Bonsoir,
Voici ce que cela donne:Capture d’écran 2021-04-18 222048.jpg
Pour les calculs matriciel j'ai utilisé WxMaxima qui est, je pense, plus précis qu'Excel:Capture d’écran 2021-04-18 222405.png
J'obtiens la courbe rouge qui ne colle pas vraiment, je vais a nouveau vérifier les calculs.Capture d’écran 2021-04-18 222441.png

[JJacquelin]

Bonjour,
Dans la seconde matrice, pouvez-vous vérifier la somme des exp(2*c*xk) que vous obtenez =5,62. Elle devrait être = 3,943 . C'est ce qui cause le mauvais résultat. A part ce chiffre, tous vos calculs sont en accord avec les miens.

[JJacquelin]

Dans le tableau Excel toute la colonne exp(2*c*xk) est fausse. Par exemple, le premier nombre ce cette colonne devrait être 1 et non pas 0,00 .

[Tartozoeufs]

Bonjour,
Il y avait bien une erreur dans toute la colonne des exp(2*c*xk).
J'aurais du m'apercevoir que ses valeurs ne ressemblaient pas du tout au carré de celles de la colonne précédente.
On obtient une courbe qui colle parfaitement aux données relevées.Capture d’écran 2021-04-19 103533.pngCapture d’écran 2021-04-19 103356.jpg
Je vais essayer de comprendre, au moins le principe de cette méthode. Merci de votre aide.

[JJacquelin]

Parfait, tout est bien qui finit bien.
Pour le principe, en résumé :

Principe.JPG

[Tartozoeufs]

Après, je coince mais je ne désespère pas.

[JJacquelin]

Au lieu de dériver, il est plus simple d'intégrer :