Somme de Riemann

[invite62c4f6a4]

Bonjour, dans le cadre d'un td on ne demande de prouver:

---

=0
-----

[JPL]

Il y a un problème avec l’image. N’utilise pas la balise IMG mais poste-la en pièce jointe.

Ou mieux, utilise la balise Tex pour écrire la formule en latex

[invite62c4f6a4]

ah oui désolé on doit prouver que cette limite est nulle

[Médiat]

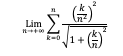
Et vous avez fait quoi (sachant que cela doit avoir un rapport avec les sommes de Riemann, d'après votre titre)

[A voir en vidéo sur Futura]

[invite62c4f6a4]

j'ai dit que la somme correspond à cette intégrale et comme l'intégrale est un réel vers +infini ca tend vers 0

[gg0]

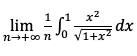
Ce n'est pas vraiment correct, ce que tu écris ici. Tu y fais l'erreur classique de passer à la limite dans une partie du calcul et pas l'autre. Mais peut-être as-tu rédigé autrement :
La limite s'écrit où Sn est une somme de Riemann qui tend vers une intégrale finie.

Cordialement.

[invite62c4f6a4]

Calculer la limite de Sn revient donc à calculer l'intégrale de 0à1 associée et l'utiliser dans le calcul de la limite de Sn*1/n, c'est ça ?

[gg0]

Oui,

c'est ça. Si tu as bien montré que est une somme de Riemann associée à une subdivision régulière de pour ta fonction. Mais pour ton exercice, on n'a même pas besoin de calculer l'intégrale. C'est un nombre fini et on applique les règles de calcul des limites.

Cordialement.

[invite62c4f6a4]

Merci beaucoup pour toutes ces informations

[jacknicklaus]

Bonsoir,

je vois pas trop l'intérêt des sommes de Riemann ici. ne suffit-il pas de remarquer que pour conclure immédiatement ?

[gg0]

Bonsoir.

Je ne vois pas comment conclure immédiatement. Mais je ne demande qu'à être convaincu. Et c'était sans doute un TD sur les sommes de Riemann.

Cordialement.

[jacknicklaus]

Mais je ne demande qu'à être convaincu. .

Ben en majorant comme indiqué, on à :

[gg0]

Ah effectivement.

Même s'il faut rajouter un terme pour que l'inégalité soit correcte. Mais ton est un équivalent.

Et ça donne une majoration intéressante, car, en multipliant par n, on retrouve la somme de Riemann : on trouve que l'intégrale est majorée par 1/2 (elle vaut environ 0,27).


Cordialement.

[jacknicklaus]

Même s'il faut rajouter un terme pour que l'inégalité soit correcte.

Ah oui, merci de le relever. Erreur d'inattention de ma part j'ai écrit par l'erreur n(n+1)/2 <= n²/2, faut l'faire !

Désolé.