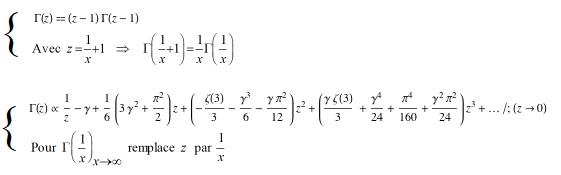Bonsoir,
La fonction
, avec
semble avoir pour droite asymptote
J'ai déjà reformuler f(x) à l'aide d'intégrales :
Donc il faudrait calculer la limite en +∞ (ou -∞) de f(x) mais je ne sais absolument pas comment m'y prendre!
Merci pour vos conseils.
Dernière modification par ph1 ; 20/04/2021 à 21h31.
Le symbolisme utilisé dans la question est des plus étonnant (et inutile).
ecriture simple de fonction.JPG
Ensuite c'est un développement asymptotique connu :
Asymptote.JPG
Il y a donc bien une asymptote y(x)=-constante d'Euler-Mascheroni = -0,577215...
Ce n'est pas 1-(pi/2) = -0,570796...
La proximité de ces deux nombres n'est qu'une simple coïncidence. Ces deux nombres n'ont rien à voir, bien que voisins.
De telles coïncidences sont très fréquentes en calcul numérique. On en voit de nombreuses et même beaucoup plus voisines les unes des autres. Au sujet de telles coïncidences, voir ce papier :
https://fr.scribd.com/doc/14161596/M...experimentales
D'accord, merci beaucoup! 1-pi/2 n'était qu'une simple supposition de ma part, erronée apparemment … Par contre dans la première PJ je ne comprends pas comment vous passez de
Et dans la deuxième PJ il est écrit :
Auriez-vous un document expliquant comment on arrive à ce résultat (que l'asymptote de
Cordialement.
On trouve ces propriétés de la fonction Gamma dans les ouvrages traitant de fonctions spéciales.
https://functions.wolfram.com/GammaBetaErf/Gamma/
https://mathworld.wolfram.com/GammaFunction.html
Voir également Wikipedia et beaucoup d'autres références.
Pour les démonstrations, il faut faire des recherches dans la littérature spécialisée.
Les limites que vous donnez sont fausses. Gamma(0) n'est pas égal à 1!=1 mais est infini. Il est bien connu que 1!=Gamma(2)=1. Donc ce n'est pas Gamma(0).
NOTE : Une faute de dactylographie dans ma réponse : Remplacer 1/x2 par 1/x dans la formule asymptotique. Pour les trois petits points, soit vous ne comprenez pas, ou vous faites semblant de ne pas comprendre, soit vous êtes rigoriste (ce qui n'est pas un défaut, mais vous devriez l'être tout autant pour vos calculs de limites ).
Oui désolé pour mon erreur sur Gamma(0). Or comme vous l'aviez dit si justement dans votre premier message
Il faut utiliser la formule asymptotique qui se trouve dans mon message précédent (23 avril, 7h45). Comme indiqué, remplacer z par 1/x dans cette formule provenant de Wolfram par le premier lien indiqué. Il y a aussi les trois petits points dans cette formule dont le symbolisme est standard et usuel. Comprenez-vous maintenant ?
Utiliser ce développement. Le reporter dans la formule de f(x). Pour la limite de f(x) les deux premiers termes suffisent car les suivants sont nuls pour x infini, c'est à dire z=0. Ceci donne la limite.
Dernière modification par JJacquelin ; 23/04/2021 à 16h26.
Pourriez vous exprimer la formule asymptotique à l'aide d'un symbole somme
Ph1,
les ... en maths comme en français courant veulent dire que ça continue mais que on n'y accorde pas d'importance (ou parfois qu'il faut bien s'arrêter dans une énumération trop longue). Comme te le dit JJ, les termes suivant ne servent pas, donc inutile de les calculer.
Maintenant, si tu veux absolument le résultat avec le symbole, fais toi-même les calculs, au lieu de demander aux autres. Et si tu as du mal à les faire, apprends les méthodes. Comme ça, tu comprendras vraiment ce qui se passe.
Cordialement.
Merci pour votre réponse gg0. Je pensais que peut-être un des termes compris dans les '...' pourrait avoir une importance non négligeable mais apparemment non, donc les premiers me suffirons. En tout cas merci à JJ pour m'avoir donné ce développement que je ne connaissait pas. Bonne fin de journée,
Cordialement.
Merci à gg0 pour le "coup de main", ou plus exactement pour le "coup de pédagogie". Ce n'est pas toujours facile dans ce genre de discussion.
Juste encore une dernière question... En partant de cette définition de la fonction Gamma (Schömilch) :
j'ai réussi à montrer que
Mon raisonnement : xxx en pièce jointe ou en LaTeX, c'est la règle. Vous demandez des efforts à vos lecteurs, fournissez-en vous aussi xxxx (c'était un peu long de tout taper en Latex).
Et désolé JJ, l'ai été un peu long à comprendre...
Dernière modification par albanxiii ; 26/04/2021 à 11h16.
L'erreur est grossière. Réfléchi à ce qu'est la différence entre deux nombres infinis. J'ai passé suffisamment de temps sur cette discussion interminable. Inutile de me poser plus de questions. Bon travail.
Oui bien sûr... désolé de vous avoir dérangé pour rien. Merci pour tout, et bonne journée.
