Lacets analyse complexe

[lesurveilleur]

Dans le cadre de mon cours d'analyse complexe, je cherche à représenter certains lacets pour pouvoir utiliser le théorème des résidus.

En rouge les lacets que je ne parviens pas à représenter.
aa.png
aaa.png
J'ai souligner un type de chaque pour ne pas trop vous solliciter.

Bien à vous.
-----

[gg0]

Bonjour.

Un traceur de courbe te donnera le tracé. Pour le premier document, tu peux traduire en coordonnées dans le plan et utiliser les tracés de courbes paramétrées. Pour le deuxième, il n'y a aucune difficulté (niveau terminale), R-t étant le module et l'argument étant constant.

NB : Je n'ai pas compris pourquoi sont soulignés en rouge des morceaux de calcul, par exemple un 2 dans 2-exp(-2it).

A savoir : pas besoin de savoir représenter, seulement vérifier que le lacet n'est parcouru qu'une seule fois, ou sinon en tenir compte.

Cordialement.

[lesurveilleur]

Je ne parviens pas à trouver un traceur de courbe paramétré complexe.

Ce qui est souligner en rouge est ce que je ne sais pas tracer.

A savoir

(*) i*t^2
Est-ce juste i veux dire qu'on est sur l'axe des ordonné et t^2 la fonction carré...
(**)Je connais R*e^2t mais pas -i*R*e^2t
(***)cos(2t) +isin(2t) serait le cercle de centre 0 et de rayon 2t ?
(****) Que signifie 2 tout seul ?
(*****) Je connais R*e^it mais pas (R-t)*e^it

Voilà ci vous pouvez m'éclaircir ou me donner un outil qui trace les courbes paramétrés...

[stefjm]

(*) i*t^2
Est-ce juste i veux dire qu'on est sur l'axe des ordonné et t^2 la fonction carré...
(**)Je connais R*e^2t mais pas -i*R*e^2t
(***)cos(2t) +isin(2t) serait le cercle de centre 0 et de rayon 2t ?
(****) Que signifie 2 tout seul ?
(*****) Je connais R*e^it mais pas (R-t)*e^it

L'outil qui va bien est le papier pour le plan complexe et le crayon pour dessiner le contour.
Comprendre ce qu'on fait est quand même indispensable...

cos^2(2t) +sin^2(2t) = 1^2, donc mélanger le rayon du cercle 1 avec le paramètre est quand même bizarre.

2 n'est pas tout seul, il est ajouté à une expression dépendante de t.

Faire des dessins dans le plan complexe pour comprendre.

[A voir en vidéo sur Futura]

[gg0]

Pas besoin de "traceur de courbe paramétré complexe", un traceur de courbes paramétrées suffit. Faut-il rappeler que le point a+ib du plan complexe est le point de coordonnées (a,b) dans le repère associé.
A voir tes questions, je commence à me demander si tu sais vraiment ce que sont les nombres complexes et comment on les représente (cours de terminale ou de L1).
Je me demande même quelles mathématiques tu as fait jusqu'ici pour écrire "Je connais R*e^it mais pas (R-t)*e^it". comme si la lettre utilisée avait une importance en maths ! R-t est un nombre (positif ici) comme R, quelle importance ?

Cordialement.

[albanxiii]

Bonjour,

Avec ceci comme base https://www.wolframalpha.com/input?i...5B0%2C+2*pi%5D vous devriez pouvoir vous débrouiller.
Ou alors si vous savez utiliser python, c'est banco !

[lesurveilleur]

Re :

Je suis parvenu à tout tracer avec geogebra MAIS je n'arrive pas à comprendre



R*e^(ipi/4) est la droite faisant un angle de pi/4 avec l'origine.

Mon intuition me pousse à dire que (R-t)e^(ipi/4) pour t allant de 0 à R est une demi droite ?

Je n'arrive pas à me la tracer au brouillon ....

Pouvez-vous m'aider ?

[gg0]

Bonjour.

"R*e^(ipi/4) est la droite ..." Non, comme R est fixé, c'est un seul nombre complexe, donc un seul point du plan. La variable est t.
Si t vraie dans R tout entier, t*e^(ipi/4) donne la droite faisant un angle de Pi/4 avec l'axe des x (ou l'axe polaire) - pas avec l'origine, qui comme tout point ne définit pas d'angle.
Si t ne fait pas tout R, on a seulement une partie de la droite, par exemple si 0<t<1, on a seulement les points d'un segment ouvert limité par 0 et e^(ipi/4) (revoir la définition géométrique du lien nombre complexe/point du plan).

Dans ton cas, tu sais où varie t, tu peux en déduire facilement où varie R-t et en déduire la courbe obtenue (ce n'est pas un lacet). Qui n'est pas une

Quand apprendras-tu où se place le nombre complexe re^(i x) dans le plan complexe ?

Cordialement.

[lesurveilleur]

Dernière question :

d.png

Le lacet est-il la partie entouré (réunion des deux cercles) ou bien tous les deux cercles ?


c.png

[gg0]

Bonjour.

Ce n'est ni le cercle entouré, ni les deux cercles, mais la réunion de deux cercles tangents de même rayon. C'est un lacet ayant un point triple. Revois le tracé du deuxième cercle.

Cordialement.

[lesurveilleur]

Bonjour,

Je vois pas ce que c'est que la réunion des deux cercles tangent de même rayon...

Est-ce l'aire des deux cercles que j'ai entouré ?

[lesurveilleur]

Ok j'ai retracé :



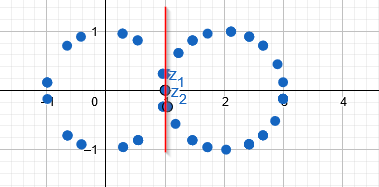
Il s'agit de la droite x=1 ?

[lesurveilleur]

Edit : problème résolu.
On tourne dans le sens direct puis indirect. C'est l'intérieur de la figure qui compte.

En revanche je ne parviens pas à tracer (R-t) * e^i(PI/4)

[gg0]

Le lacet est la courbe paramétrée, pas l'intérieur.

Pour (R-t) * e^i(PI/4) , ça se fait à la main. Comme t varie entre 0 et R, R-t est positif, variant de R à R-R = 0; donc ce sont tous les complexes d'argument Pi/4 et de module compris entre 0 et R. Ça fait un segment évident.