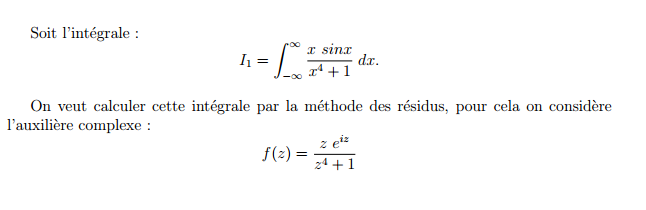Bonjour, je commence cette année l'analyse complexe et je bloque sur deux trois choses d'un exercice type.
On souhaite calculer une intégrale à l'aide d'une fonction complexe qui lui est associée:
L'ennoncé me demande de déterminer les singularités associées, ce que je fais. (4 points, chacun à l'intérieur d'un des quarts du cercle de rayon 1).
Puis il me fait calculer l'intégrale I' de la fonction complexe sur un contour composé du segment réel [-R;R] et du demi-cercle supérieur de rayon R. (Ok, je trouve une certain valeur). Puis il me fait majorer l'intégrale du demi-cercle par quelque chose qui tend vers 0 pour R -> infini.
A partir de là je dois en déduire la valeur de mon intégrale réelle I1.
Je connais la réponse mais je n'en saisis pas le sens. La réponse est I1=Im(I')
Je n'arrive pas à saisir le sens de cette réponse. Au final ce que j'ai calculé précedemment est l'intégrale de la fonction complexe sur le segment [-R;R], mais quel est le lien entre l'intégrale sur ce segment et l'intégrale réelle? Pourquoi n'ai-je au final intégré que deux singularités? (celles du demi-cercle supérieur) Pourquoi avoir pris le segment réel et pas le segment imaginaire?
-----