Bonjour,
Je n'ai pas du tout compris la réponse de cette question sur les portraits de phase.
Je travaille sur le système :
dx/dt = y
dy/dt = 2x-y
avec les conditions initiales :
x(t=0) = x0
y(t=0)=y0
Je réécris ce système sous la forme dX/dt = AX
Dans les questions précédentes, nous avons les valeurs propres λ1 = -2 et λ2 = 1, et avons choisi u1 = (1, -2) et u2 = (1, 1)
Sur le schéma en PJ, je dois représenter le portrait de phase du système, et tracer les vecteurs propres u1 et u2. J'ai colorié u1 en bleu, et u2 en vert.
J'ai appris qu'il y a stabilité si les 2 valeurs propres sont négatives. Ici, l'une des deux valeurs propre est >0, donc X* est instable...
Cependant, je ne comprends pas du tout les autres courbes, et leur "flèches".
Pouvez vous m'éclairez s'il vous plait ? J'ai un peu de mal avec cette partie du cours
Merci de votre aide !
1 PJ :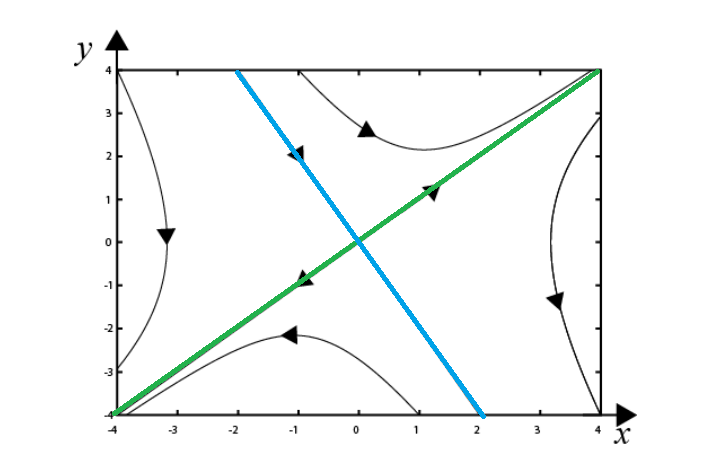
-----


