Intégrale

[Ikgn]

Bonjour, ca fait un moment je peine a terminer un exercice sur les intégrales, si quelqu'un pouvait me donner juste une piste s'il vous plaît
(La dernière 👇&#127996

-----

[GBZM]

Bonjour,
Pour le premier exercice on te donne le contour d'intégration à utiliser : on part de près de - l'infini sur l'axe réel, on suit l'axe réel en contournant 0 par un petit demi-cercle au-dessus, on arrive près de + l'infini et on fait un grand demi-cercle dans le demi-plan supérieur qui nous ramène vers - l'infini.
Il faut regarder la détermination de la fonction à intégrer et voir le(s) résidu(s) dans le domaine.

[jacknicklaus]

Bonjour

je suppose que tu connais la méthode des résidus.
Pour le a) tu peux montrer facilement (changement de variable) que la somme de -infini à +infini vaut exactement 2 fois la somme demandée (0 à + infini). Il te reste à choisir le bon contour. Le lemme de Jordan montrera que la partie en demi-cercle à l'infini donne une contribution nulle. Reste à calculer le résidu donné par l'unique racine de z²+1 = 0 contenue dans le contour. Stricte application du cours.

[GBZM]

Hum hum, il faut faire un peu attention à la détermination du logarithme !

[A voir en vidéo sur Futura]

[jacknicklaus]

tiens c'est amusant, pour le b), le même changement de variable que pour le a) montre immédiatement que l'intégrale vaut zéro.


@GBZM : oui !

[GBZM]

Le changement de variable que je vois pour le b), c'est plutôt . Et il n'y a alors pas besoin de résidu.

[jacknicklaus]

Le changement de variable que je vois pour le b), c'est plutôt . Et il n'y a alors pas besoin de résidu.

oui tout à fait, c'est bien ce que je dis au #5. ("montre immédiatement")

[GBZM]

Tu parles du "même changement de variable que pour le a)" ????
Ce que tu racontes pour le a) n'est d'ailleurs pas très clair puisque tu parles de l'intégrale de à d'une fonction avec dedans.

[jacknicklaus]

Tu parles du "même changement de variable que pour le a)" ????.

oui tout à fait . celui là :

Bonjour
Pour le a) tu peux montrer facilement (changement de variable) que la somme de -infini à +infini vaut exactement 2 fois la somme demandée (0 à + infini).

où on utilise aussi x -> 1/x.

Et en effet, je n'ai pas détaillé la manière de procéder autour de 0, que tu avais déjà évoqué dans ton message #2, en détaillant le contour à utiliser.

Faut quand même laisser du grain à moudre pour Ikgn... C'est la limite de l'exercice : en dire suffisamment pour aider, mais pas trop non plus.

[GBZM]

Franchement, je ne comprends pas ce que tu racontes. Ikgn le comprendra-t-il ?
Tu parles de l'intégrale de à de quelle fonction ?? Si c'est , alors vu que c'est une fonction paire il n'y a besoin d'aucun changement de variable (et sûrement pas de !) pour voir que l'intégrale de à est deux fois celle de 0 à .

[Ikgn]

Merci pour vos interventions, mais pour la première et la 2 ème je n'ai pas eu tellement de difficulté, j'ai utilisé le théorème de résidu sur deux demi-cercles le premier de -r a r et le deuxième de -£ a £ en faisant tendre r vera l'infini et £ vers 0 avec le lemme de jordan ca donne 0 encore ensuite un petit changement de ln(x)=ln(-x) +iπ pour gerer la partie négative finalement je trouve les 2 résultats c'est le 3 eme qui me pose problème je ne sais pas quoi

Le changement de variable mentionné me semble assez intéressant je vais l'essayer, ca pourra peut-être me servir pour autre cas

utiliser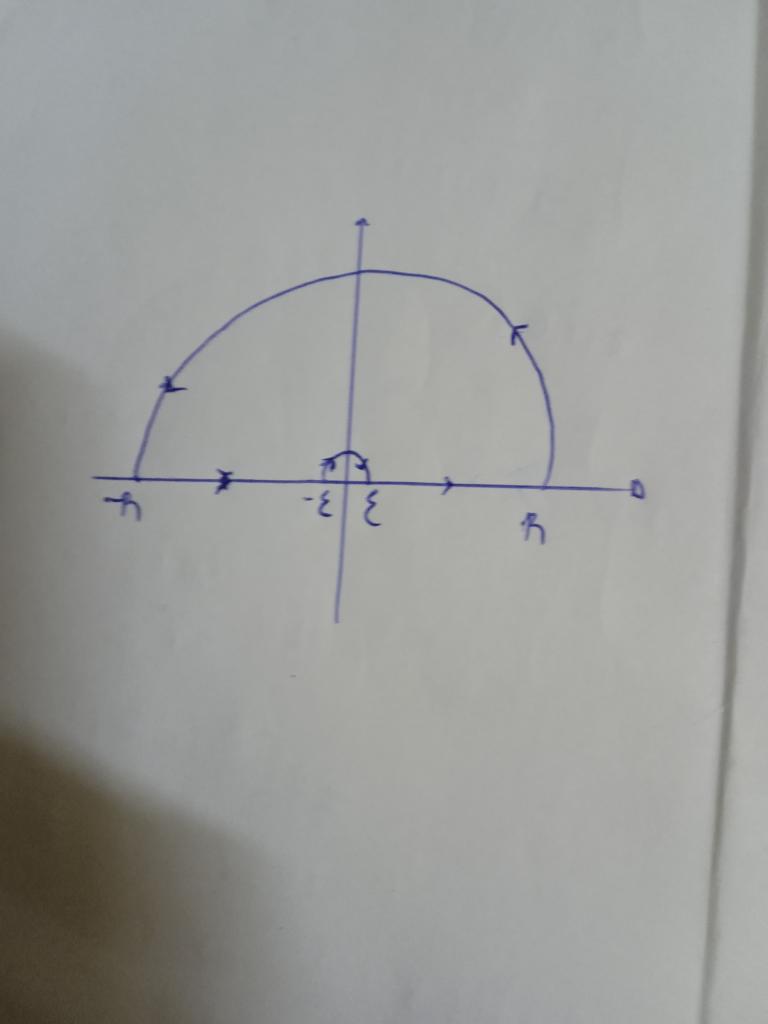

[5t3ph]

Moi aussi j'ai dû passer par un ln(-x) quand x>0 et j'ai poursuivi que c'était egal à iπ + ln(x). Je pense que c'est valide, j'arrive bien au résultat annoncé 🙄

Pour la dernière intégrale, intuitivement je pense à un changement de variable pour basculer vers des fonctions trigonométriques mais je n'ai pas poussé l'idée 🙄

Je aussi preneur de toute indication 🙂

[GBZM]

Pour le deuxième exercice, le domaine est la sphère de Riemann privée du segment de l'axe réel. La détermination de sur ce domaine est celle qui vaut en .
On prend comme contour un aller-retour sur le segment , un peu au-dessus de gauche à droite et un peu en-dessous de droite à gauche, avec des petits cercles autour de et de pour faire les demi-tours.
On a des résidus en et à l'infini.

[GBZM]

Un petit dessin :

[5t3ph]

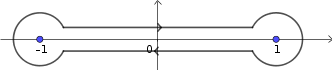
Tes indications étaient très claires GBZM, merci
Une valeur approchée de l'aire par Geogebra confirme mon résultat, .




Par contre, ça fait bousiller un peu de papier, c'est très calculatoire

[GBZM]

D'accord avec ce que tu trouves. C'est le résidu en l'infini qui demande un peu d'attention, mais ce n'est pas si compliqué que ça.