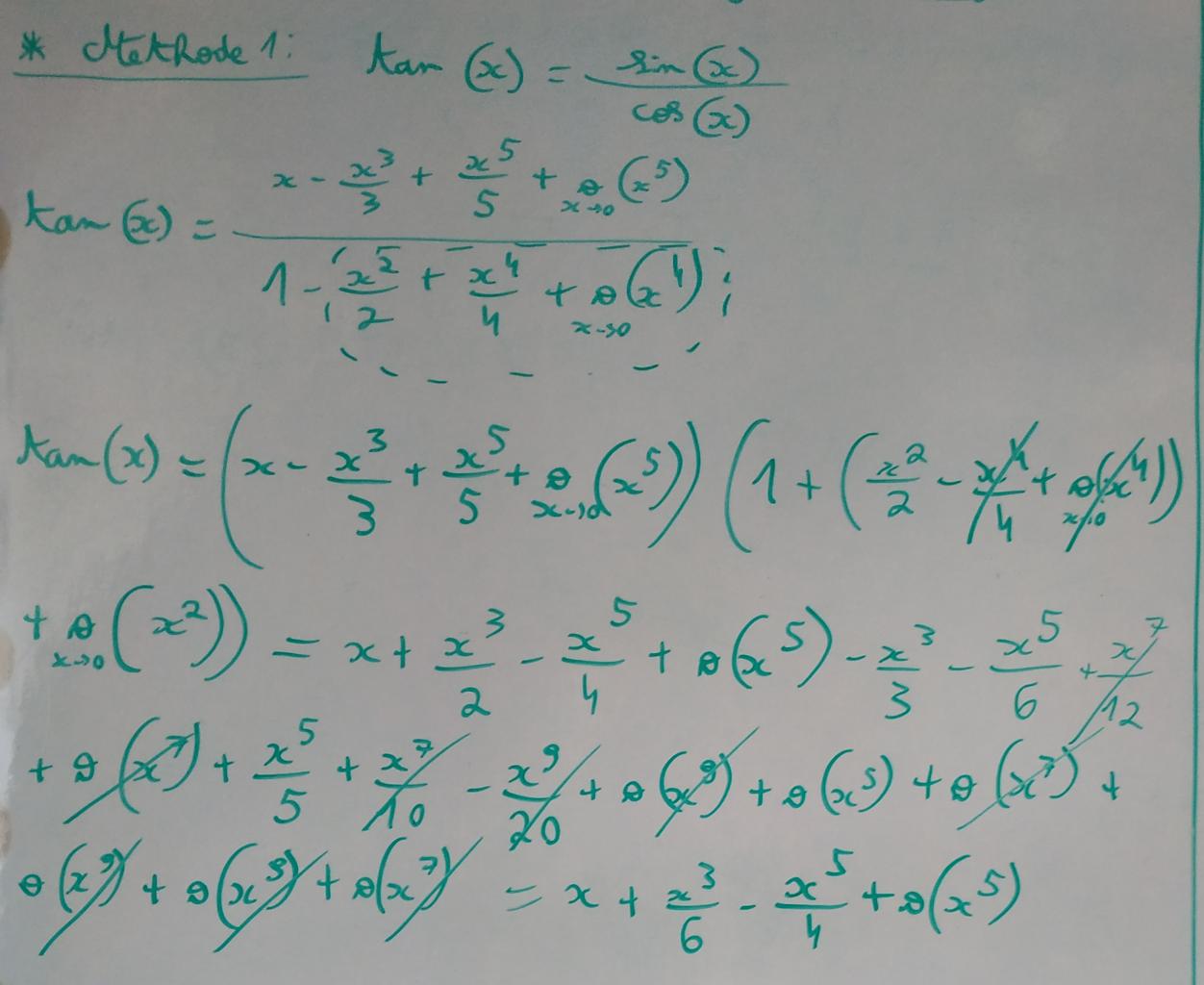Bonjour, j'essaie de retrouver le DL de la fonction tangente en 0 à l'ordre 5 en partant de sin(x)/cos(x) mais je bloque pour savoir que vaut:
.
J'ai pensé à ce que cela vaille:
Mais pour moi c'est faux, toute façon je n'arrive pas au bon résultat. Quelqu'un pourrait-il m'aider ?
Merci d'avance à tout personne m'accordant un peu de son temps.
Bonjour.
Ton terme est bien un o(x²) comme la définition te permettrait de le prouver. On peut aussi remarquer que les deux autres termes étant négligeables par rapport à x², seul le premier terme compte.
Je serais curieux de savoir pourquoi tu dis "pour moi c'est faux".
Sinon, pour un DL à l'ordre 5, tu as besoins de DL à l'ordre 5 de sin et cos (puisque cos (0) n'est pas nul), puis d'appliquer la règle sur les quotients de DL. donc à priori, tu n'as pas ce genre de problème.
Cordialement.
D'accord, je vous remercie. Je pensais que c'était faux parce que je n'arrivais pas au bon résultat final mais mon erreur est plus loin.
Je n'arrive pas à obtenir le bon DL. Où seraient mes erreurs ?
J'ai appliqué le DL de 1/1+X à l'ordre 1 en 0.
DL d'ordre 1 à qui tu fais manger des termes d'ordre 5 en oubliant les termes 2,3,4 et 5 ?
Ça doit être faisable avec une division suivant les puissances croissantes.
Sinon, il faut développer à l'ordre 5 et ça me parait un peu chiant.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Apparemment, tu ne connais pas la règle sur le quotient de deux DL. Ça donne immédiatement le résultat.
Ton erreur est au début, de vouloir obtenir un DL d'ordre 5 en utilisant un DL l'ordre 2 !! Il faut être sérieux. Si tu veux un DL final d'ordre 56, il te faut des DL d'ordre 5 à multiplier, que tu obtiendras en développant 1/(1+X) à un ordre suffisant. Et c'est facile de voir comment.
En tout cas, tu as totalement triché dans ton développement du produit, en ne reprenant pas le o(x²) de la fin quand tu as développé. Ça fait une deuxième erreur, qui t'a empêché de voir exactement comment faire.
Cordialement.
Ah d'accord, du coup le DL de 1/(1+X) je dois le faire à l'ordre 5 ?
Quelle est mon erreur à la fin même si c'est déjà faux ?
À la fin, tu as oublié de multiplier le o(x^2).
Et si tu essaies vraiment de faire le calcul, tu verras que 5 n'est pas nécessaire.
Rappel : inutile d'écrire des termes négligeables par rapport à x^5, ils sont tous dans le o(x^5).
D'accord je vous remercie pour votre aide.
