Bonjour,
Est-ce qu'il existe une règle selon laquelle n'importe quel premier P peut s'exprimer comme la somme de deux multiples de nombres premiers différents de deux ?
P3 = P1.x + P2.x
x≠2
Comme par exemple 23 = 5x1 + 3x6
Merci
-----

Bonjour,
Est-ce qu'il existe une règle selon laquelle n'importe quel premier P peut s'exprimer comme la somme de deux multiples de nombres premiers différents de deux ?
P3 = P1.x + P2.x
x≠2
Comme par exemple 23 = 5x1 + 3x6
Merci
Dernière modification par Casper75 ; 16/06/2023 à 13h33.

Bonjour.
Ta règle est un peu floue. Si tu considères que les multiples d'un premier p sont les k*p avec k>0, ça coince pour 3, et ça a de fortes chances d'être vrai pour les autres premiers. Comme tu admets 1p comme "multiple d'un premier", tu considères, pour un nombre premier p>3 le nombre p-3, qui est un multiple de 2 : p = 1.3+k.2
Voilà, tu as ta réponse.
Pourquoi cette question ?

Bon je ne peux pas editer. En fait je veux plutôt savoir si 'il existe une règle selon laquelle n'importe quel premier (superieur à 3) peut s'exprimer comme la somme de deux nombre (different de deux) dont l'un est premier et l'autre multiple de premier.
premier = premier + Premier.x
x≠2
Comme par exemple 23 = 5 + 3x6
C'est juste par curiosité
Dernière modification par Casper75 ; 16/06/2023 à 13h57.

oui et c'est évident : tu choisis n'importe quel nombre premier p plus petit que x, alors le nombre x-p a un facteur premier q (car tout nombre a au moins un facteur premier) et donc x-p = aq et x = p + aq

J'ai déjà répondu au message #2 : p est la somme de 3 (un premier) et d'un multiple d'un premier.

Ok mais je veux que le nombre premier soit additionné à un multiple de premier autre que deux, et multiplié par un nombre different de deux
En faisant 23 = 3 + 20 le nombre 20 est multiple de 2
Dernière modification par Casper75 ; 16/06/2023 à 14h41.

malheureusement pour toi, si tu écris x = p + n où x et p sont premiers >2 alors n est nécessairement un multiple de 2 (démontre-le).

Remarque : Changer la question à chaque fois qu'on y a répondu montre un manque de réflexion personnelle préalable.
"Ce qui se conçoit bien s'énonce clairement" Nicolas Boileau.

en revanche sauf dans les quelques cas particuliers où x-p est une puissance de deux comme 11 = 3+8 , x-p est aussi un multiple d'un nombre différent de deux donc en général la réponse est oui.

En fait, le seul cas embêtant est lorsque n-3 est une puissance de 2. Pour n suffisamment grand, n-5 ne sera pas une puissance de 2. Ça arrive dès que les puissances de 2 ont plus de 2 d'écart, donc lorsque n-3>4. Il ne reste donc à tester que 5 et 7, pour les autres nombres premiers, n-3 ou n-5 est de la forme k.p où p est impair (et k pair).

Pas forcément dans le sens ou tout à chacun ne peut avoir le temps de re-découvrir, depuis sa propre connaissance, tout ce qui a déjà été fait dans le domaine.
Sans questions il n'y a que des problèmes sans réponses.


Liet Kynes,
tu confonds le manque de connaissances avec le manque de réflexion.


Ok merci pour vos réponses. J'essayerais de mieux réflechir avant de poster. J'ai voulu supprimer il était trop tard et j'ai oublié des infos dans le repost.. PAr ailleurs je ne pratique pas du tout les maths et j'ai seulement un attrait pour les nombres premiers, merci d'être indulgent
-----------------------------------
Autre Question ( plus corsé ):
J'aimerais trouver une valeur de N pair et les nombres premiers X, Y, et Z tel que ces égalités se vérifient
Un jour j'ai trouvé en cherchant à taton, mais je n'ai aucune idée de comment chercher normalement.
Merci

Bonjour,
C'est très louable de s'intéresser aux nombres premiers, mais fais au moins l'effort d'utiliser des notations correctes !
Que signifie "X^?" ??
Parles-tu de puissance de X ou de multiple de X ?

Mince c'est la catastrophe je voulais dire multiplier.
Vraiment je suis desolé je n'ai tellement pas les codes, surtout sur ordi, j'ai confondu l'usage du point/ ou asterix avec ^ qui visiblement sert uniquement pour les puissances.
Vraiment la honte.
--------------------------------------------------
Je re-poste ici ma question rectifié :
J'aimerais trouver une valeur de N pair et les nombres premiers X, Y, et Z tel que ces égalités se vérifient
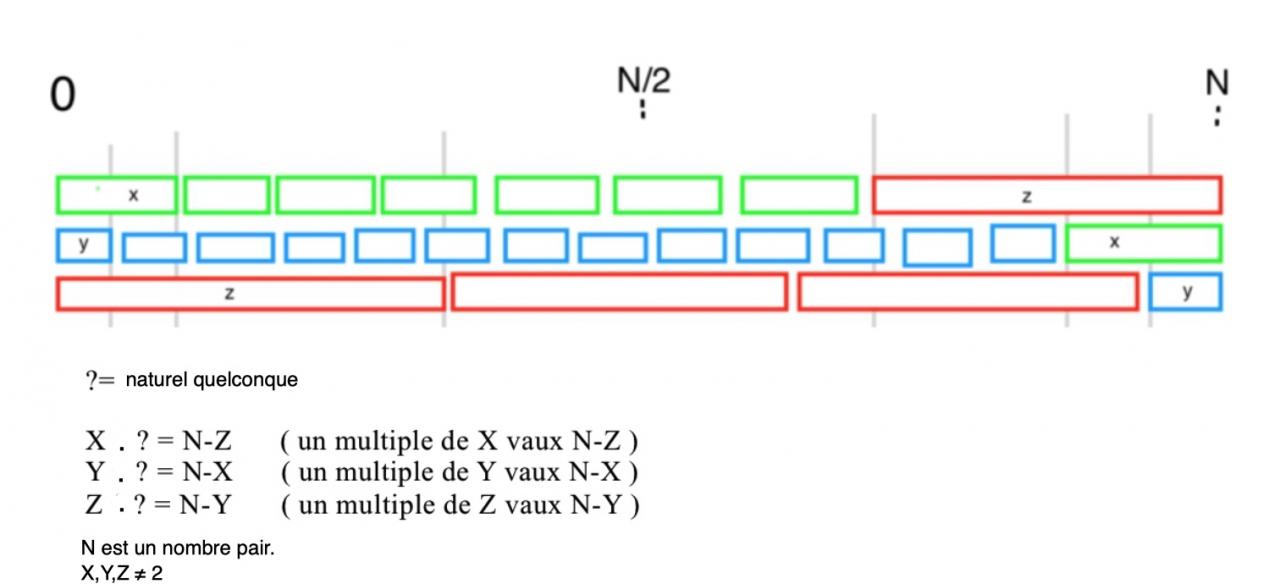

Bonjour.
En fait, tu ne cherches pas seulement 4 nombres, mais 7, avec les 3 que tu as remplacés par des "?".
Tu dis que tu en as trouvé un exemple par tâtonnements, peux-tu le donner ? C'est important, car ça signifie que la question a des réponses.
Au fait, as-tu compris les preuves pour ta première question ?
Cordialement.

il y a des solutions triviales avex X=Y=Z , N = (k+1)X et ? = k

Oui merci, j'ai bien compris la réponse à ma première question.
Les point d'interrogations peuvent être vu comme 3 inconnus supplémentaires en effets je suppose.
J'avais bien trouvé une solution en essayant plein de combinaisons sur une feuille remplit de colonnes de nombres premiers, presque par miracle
En re-essayant j'ai réeussit à trouver mais seulement avec N impair. (Les x et y ne sont pas dans le même ordre mais le principe reste le même)
N=33
y=5
x=7
z=13
x.? = N-y
y. ? = N-z
z. ? =N-x
7x4 = 33-5
5x4 = 33-13
13x2 = 33-7
Dernière modification par Casper75 ; 19/06/2023 à 19h59.

En commençant par chercher la même chose avec seulement deux nombres x et y j'ai trouvé une petite astuce.
x. ? = Z -y (un multiple de x vaut Z-y)
y. ? = Z -x (un multiple de y vaut Z-x )
On peut choisir aléatoirement que
x= 5 y=7
Et sachant qu'autour de leur multiples commun, les multiples sont réparti symétriquement
Alors on peut trouve N en faisant :
N= (5X7) + (5+7)
N=47
ON essaie 47 - 7= 40 qui est un multiple de 5
47- 5 =42 qui est un multiple de 7
Mais avec plus de deux nombres je ne sais pas comment faire

N pair ou impair ?

Sans questions il n'y a que des problèmes sans réponses.

Il me semblait que N pair était une donnée initiale du problème :
Alors finalement, N pair est une contrainte donnée du problème ?J'aimerais trouver une valeur de N pair
Si oui, pourquoi ?
Si non, ok.
Dernière modification par Merlin95 ; 20/06/2023 à 08h28.

OUi N pair est une contrainte parce-que la base de ma reflexion c'est la conjecture de goldbach en gros... sans rentrer dans les détails.
Mais si tu as une manière de trouver avec N impair c'est deja interessant

