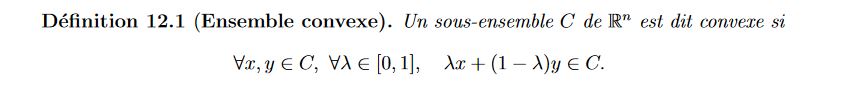Le retour des topos - categories et ensemble

[pachacamac]

Bonjour,

Je suis content qu'en français courant on puisse quand même parler de l'ensemble des ensembles

@gg0 : Dans une théorie des ensembles donnée, le mot "ensemble" n'a pas de signification.

Je te crois sur parole vu notre différence de niveau en mathématiques mais je trouve ça bizarre...

Sinon j'ai compris le raisonnement en #22 mais j'en ai trouvé un autre qui mène à une conclusion différente, je le soumet à votre sagacité...

Imaginons par une expérience de pensé que nous fassions une collection de tous les ensembles sans y mettre l'ensemble de tous les ensembles ( puisque celui ci n'existe pas d'après #22 et les mathématiciens) .
Puis comme en #22 on sépare cette collection d'ensembles en ceux qui se contiennent eux même que nous regroupons dans un ensemble A et ceux qui ne ce contiennent pas eux même que nous regroupons dans un ensemble B.

Ces deux ensembles sont bien évidemment exclusifs : un ensemble est soit dans A soit dans B

Mais qu'est qui nous empêche de créer un nouvel ensemble C = A U B (A union B) qui serait donc l'ensemble de tous les ensembles ?

Vu que je pense pas avoir fais une nouvelle découverte mathématique je me demande ce qui cloche dans ce raisonnement ?
-----

[gg0]

Toujours le même problème. Où placer B ? Dans A ou dans B.
En fait, le problème peut devenir très concret : Un bibliothécaire possède des ouvrages, des catalogues d'ouvrages, et veut tout cataloguer. Il décide de faire des catalogues de romans, des catalogues de catalogues, etc. Il finit par faire un catalogue global, puis, inspiration diabolique, de partager ce catalogue global avec d'abord un catalogue de tous les ouvrages qui ne se citent pas eux-même, ensuite un catalogue des ouvrages qui se citent eux-mêmes. Ce dernier se citera, évidemment, mais l'autre, où le cataloguer ? Paradoxe.

Attention, dans ces questions, la notion intuitive d'ensemble n'est pas très efficace, car elle recouvre des notions différentes, les ensembles, et ce que les mathématiciens appellent des classes (collections).

[pachacamac]

J’annule ma question, j'ai trouvé la faille...

Si C = A U B alors C est obligatoirement inclu dans A ou dans B et donc ça nous ramène au début de la démonstration en #22.

[pachacamac]

Euréka..
Il existe une Classe de tous les ensembles

Merci de m'avoir indiqué cette piste

[oualos]

Attention, dans ces questions, la notion intuitive d'ensemble n'est pas très efficace, car elle recouvre des notions différentes, les ensembles, et ce que les mathématiciens appellent des classes (collections)

.
Pardon pour une question encore une fois naïve mais la collection étant une définition elle s'auto-justifierait pour parler un langage disons plus terre-à-terre ?
La définition d'un concept ou entité en maths n'est-elle pas identique ou du même ordre, disons similaire à celle d'un axiome dans le sens où elle est auto-référentielle ?
Merci de votre réponse cela m'aidera à mieux comprendre: les mathématiques sont loin et la théorie des ensembles est particulièrement abstraite dans mes souvenirs, justement comme vous le mentionnez car il y a plusieurs définitions.

[gg0]

Je ne suis pas assez calé en maths pour donner des éléments précis, d'autant que pour l'essentiel des maths, la théorie "naïve" des ensembles suffit largement. Peut-être un logien passera-t-il ?
Sinon, je ne comprends pas une bonne partie de ce que tu dis :
" la collection étant une définition" ??? Ça n'a aucun sens pour moi
"La définition d'un concept ou entité en maths" ??? Je ne vois pas où on trouve ça. Au départ, on a des axiomes, utilisant des mots (*) non définis. Par exemple, dans l'axiomatique de Hilbert de la géométrie, les mots "point", "droite", "plan". Et on définit les relations entre ces mots. Puis on définit des objets plus complexes à partir de ce qu'on a.
"s’auto-justifierait", "elle est auto-référentielle" ??? je ne comprends pas où est l'autoréférence. Ni le besoin de "justification" des axiomes.

Cordialement.

(*) pas des concepts. Après, on peut noter que telle ou telle autre situation revient à ça, même si ce n'était pas l'idée de départ, le "concept" comme tu dis, qu'on a traduit. par exemple l'interprétation de la géométrie plane classique par les couples de réels comme points.

[pachacamac]

J'ai l' impression qu'au début des raisonnement mathématiques il y a des axiomes et des définitions.

La définition d'un concept ou entité en maths" ??? Je ne vois pas où on trouve ça.

Facile...
Par exemple, les axiomes d'Euclide genre : par deux points il ne passe q'une droite : ce sont des axiomes parce que ce sont des "vérités " que l'on prend comme point de départ et qu'on ne peut démontrer.

Par contre qu'est ce qu'une injection, surjection, bijection, un groupe un corps ou un anneau me semble relevé de définitions.

la théorie des ensembles est particulièrement abstraite dans mes souvenirs

Dans mes souvenirs de collège, j'ai trouvé l'introduction à la théorie des ensembles avec ses diagrammes de Venn plutôt facile, je n'en dirais pas autant de la théorie des catégories..

[oualos]

J'ai l' impression qu'au début des raisonnement mathématiques il y a des axiomes et des définitions.

C'est aussi mes souvenirs.
Tu fais référence à Euclide et l'exemple qui m'est resté en mémoire, à beaucoup de gens sans doute, c'est qu'après avoir éliminé le cinquième axiome on s'est mis je crois à parler de postulat ce qui introduit un sens nettement plus nuancé et intègre la notion de constructivisme pour une géométrie à partir de points de départ nommés postulats et non plus axiomes.
Je suis pas assez calé mais je crois qu'à partir du XVIIIème- XIXème siècle on commence à s'interroger sur les points de départ de la géométrie, de l'algèbre, de la logique voire de l'analyse (?)
Et du coup à en inventer d'autres, surtout des géométries comme Gauss et Lobachevsky lequel définit le parallélisme comme relation d'équivalence avec symétrie et transitivité.
Merci de corriger ou rectifier

[gg0]

Attention aux idées trop simples :

"ce sont des axiomes parce que ce sont des "vérités " que l'on prend comme point de départ et qu'on ne peut démontrer." Ce qui est correct, c'est seulement : "ce sont des axiomes que l'on prend comme point de départ." Le reste est de l'habillage, soit pour la présentation aux collégiens, soit par des vulgarisateurs malhabiles. La notion de "vérité" n'a pas de sens en dehors d'une théorie (*); et si A est l'un des axiomes, A==>A démontre bien A (à partir des axiomes acceptés).
"après avoir éliminé le cinquième axiome on s'est mis je crois à parler de postulat". Non, le mot "postulat" (en version grecque) est dans le texte des éléments d'Euclide, avec le sens actuel du mot "axiome", c'est à dire de propriété qu'on ne peut démontrer. Les axiomes (ou "notions ordinaires") d'Euclide sont plutôt des "vérités générales", indépendantes de la géométrie, parlant d'égalité ou non ("le tout est plus grand que la partie"). Voir éléments et Livre I.

Pourquoi ne pas étudier sérieusement l'histoire des sciences et en particulier des maths ? Plutôt que d'en parler sur le mode "J'ai pas lu, j'ai pas vu, mais j'ai entendu parler" (rubrique de Cavana dans Charlie Hebdo). Avec Internet, on a des tas de références et même des textes entiers ...

NB : Je n'ai pas tout corrigé ou rectifié, tout est mélangé.

[oualos]

ok pour la vérité toute la vérité rien que la vérité

Selon Wiki, le postulat (du latin postulare qui signifie « demander ») est un principe non démontré utilisé dans la construction d'une théorie mathématique.
Toujours selon lui, un axiome (en grec ancien : ἀξίωμα /axioma, « principe servant de base à une démonstration, principe évident en soi » – lui-même dérivé de άξιόω (axioô), « juger convenable, croire juste ») est une proposition non démontrée, utilisée comme fondement d’un raisonnement ou d’une théorie mathématique.

C'est vrai que la différence ne saute pas aux yeux. Et pourtant... le postulat fait référence à la construction, l'axiome non! Bref ne chipotons pas, ça revient quasiment au même.
Les puristes comme d'habitude trancheront.
L'un est en grec ancien et l'autre en latin: donc on a toutes les raisons de penser que le latin étant restée la langue savante pendant longtemps en Occident -au moins après Descartes Leibniz Spinoza voir le fameux cogito ergo sum traduit en introduisant le "Je" en français qui n'existe pas en latin-, le terme de "postulat" est apparu après celui d'axiome, terme grec indubitablement.
En tout cas vu la tonne d'écrits philosophiques produits sur le fameux cogito dont Kant, on pourrait tout de même penser que concernant Descartes, cette histoire de traduction a une importance.
Et donc le postulat est postérieur comme terme à axiome et historiquement le sens n'est pas le même si on veut chipoter...
Mais comme je n'y tiens pas du tout (à chipoter) laissons tomber cette querelle de traduction et de signification qui varie au fil du temps, trop compliqué!
On a tous les deux été dans l'inexactitude, moi bien plus que vous bien sûr

[gg0]

Je n'ai pas chipoté, j'ai rappelé le sens des mots chez Euclide. Dans les maths actuelles, on n'utilise plus le mot "postulat". Et dans la version moderne de la géométrie euclidienne, par exemple celle de Hilbert, il n'y a que des axiomes, qui reprennent en partie les postulats d'Euclide (bien incomplets, en fait).
Si tu tiens vraiment à chipoter, lis Euclide en grec (ancien), tu verras bien les mots qu'il emploie ...

[pachacamac]

Bonjour,

Je pense qu'on est globalement d'accord sur ce qu'est un axiome même si je me suis mal exprimé en #37 (bien que j'ai mis le mot "vérité" entre guillemets.. )
Donc inutile de chipoté d'avantage là dessus

Par contre sur la primauté entre axiomes et définitions j'ai trouve étonnante la question/remarque de gg0.

La définition d'un concept ou entité en maths" ??? Je ne vois pas où on trouve ça

.

J'ai l'impression qu'il y en a partout.

Par exemple si on prend comme entité mathématique les nombres premiers

il me semble qu'en premier, en préliminaire à l’étude de toutes leur propriétés, il faut d’abord les définir. Cette définition des nombres premiers ne me semble pas être un axiome.


Et cela me semble vrai presque partout en math

Si on veut étudier les ensembles convexes, un bon cours commencera par leur définition



Là aussi je vois une définition mais pas d'axiome.

Merci

[gg0]

Ah, je n'avais pas compris, le mot "entité" n'est pas un mot mathématique, et le fait de parler d'auto-référentiel ne me permettait pas de comprendre. Surtout qu'il n'y a pas d'auto-référence dans la définition des nombres premiers ou de sous-ensemble convexe.
En maths, une définition est simplement une abréviation, elle ne donne pas d'existence nouvelle, elle sert à parler plus rapidement. L'adjectif "premier" est plus court que "qui a exactement deux diviseurs" (et je n'essaie pas pour "convexe", c'est trop long). les nombres dits "premiers" préexistent à leur définition, et, avec ZFC comme théorie de base et les ordinaux, on définit les entiers, mot simplificateur pour "ordinaux finis", la multiplication (je passe, c'est compliqué, mais le mot n'est qu'une abréviation), le mot "diviseur (abréviation encore) et "premier". Les seuls axiomes utilisés sont ceux du système ZFC. Après, il y a des définitions (abréviations) et démonstrations (qui donnent des théorèmes).
Les maths fonctionnent comme ça.

[pachacamac]

Okay.
Note que c'est pas moi qui parle d'auto référencement (je vois pas trop ce que cela veut dire ) dans le cas de la définition des nombres premiers ou d'ensembles convexes.

Sinon je pense qu'avec la discussion sur les axiomes on s'est trop éloigné de la question initiale de ce fil donc à mon avis ont peut le fermer...

[pachacamac]

@gg0

Aussi, pour boucler la boucle, j'ai encore une petite question concernant les catégories et les axiomes.

J'ai lu sur un cours que les catégories étaient définies comme un systèmes axiomatique...et sur wikipedia il y a une définition des catégories utilisant 6 critères.

Je serai curieux de savoir si ces critères sont plutôt des définitions ou des axiomes..




Merci

[GBZM]

Un groupe est une structure algébrique vérifiant certains axiomes;
Une catégorie, c'est pareil : une structure algébrique vérifiant certains axiomes

[pachacamac]

Ok et Merci

[gg0]

La définition d'un groupe se fait par la donnée d'un couple (ensemble/loi de composition interne) vérifiant 3 propriétés, appelées axiomes du groupe.
Pourquoi "axiomes" : parce que si on sait que (G,^) est un groupe, les axiomes sont "vrais" (on peut les utiliser). par exemple, pour trois éléments g, h, i du groupe, on sait que g^(h^i)=(g^h)^i (*).
Mais si on veut démontrer qu'un couple (H,£) est un groupe, on n'a pas d'axiome, et on va même démontrer que les trois propriétés sont vraies, elles deviennent des théorèmes.
Voilà l'usage actuel du mot axiome.

(*) attention, ici, ^ n'est pas un symbole de puissance, juste la notation de la loi de composition interne du groupe.

[pachacamac]

Merci, c'est limpide.

[oualos]

Ah, je n'avais pas compris, le mot "entité" n'est pas un mot mathématique, et le fait de parler d'auto-référentiel ne me permettait pas de comprendre. Surtout qu'il n'y a pas d'auto-référence dans la définition des nombres premiers ou de sous-ensemble convexe.
En maths, une définition est simplement une abréviation, elle ne donne pas d'existence nouvelle, elle sert à parler plus rapidement. L'adjectif "premier" est plus court que "qui a exactement deux diviseurs" (et je n'essaie pas pour "convexe", c'est trop long). les nombres dits "premiers" préexistent à leur définition, et, avec ZFC comme théorie de base et les ordinaux, on définit les entiers, mot simplificateur pour "ordinaux finis", la multiplication (je passe, c'est compliqué, mais le mot n'est qu'une abréviation), le mot "diviseur (abréviation encore) et "premier". Les seuls axiomes utilisés sont ceux du système ZFC. Après, il y a des définitions (abréviations) et démonstrations (qui donnent des théorèmes).
Les maths fonctionnent comme ça.

Oui j'ai compris
Les mathématiques sont tautologiques et vides de sens: c'est pour cela qu'elles sont universelles dirons-nous.
Il n'a pas de polysémie comme avec le langage et les maths sont monosémiques. On ne se dispute pas sur le sens d'un mot: par contre les histoires de traduction comme du grec vers le latin peuvent "juste" se révéler intéressantes.
Et on les laisse tomber après évidemment car ça sert pas aux maths ni aux mathématiciens d'après ce que tu expliques! Je comprends parfaitement.
On va pas s'attarder sur cette discussion en particulier mais chatGPT qui fait des erreurs en sciences, en littérature et en histoire -c'est bien connu je l'ai expérimenté aussi en informatique qui est plus mon domaine- donc à surtout pas rendre comme référence nec plus ultra de la "vérité", il dit cela.

Question: quelle différence entre un axiome et un postulat ?


ChatGPT
Les termes "axiome" et "postulat" sont souvent utilisés de manière interchangeable, mais ils ont des nuances subtiles de sens dans différents contextes. En général, ils désignent tous deux des énoncés de base ou des principes fondamentaux sur lesquels est intégré un système de connaissances, comme une théorie mathématique ou une philosophie. Cependant, il y a des différences légères dans la manière dont ces termes sont compris :

Axiome : Un axiome est un énoncé qui est généralement considéré comme évident, auto-évident ou indiscutable au sein d'un certain système de pensée. Les axiomes sont souvent utilisés comme points de départ pour déduire d'autres vérités ou conclusions. Ils sont souvent perçus comme des vérités établies et acceptées sans nécessiter de preuves. En mathématiques, les axiomes forment la base des théories et des démonstrations.

Postulat : Un postulat est également un énoncé de base, mais il peut être formulé comme une hypothèse ou une assertion qui est posée pour être vraie, mais qui pourrait ne pas être immédiatement évidente. Les postulats sont parfois utilisés pour introduire des idées ou des concepts de départ qui sont nécessaires pour développer une théorie, même s'ils ne sont pas aussi strictement considérés comme indiscutables que les axiomes.

En somme, la distinction entre les deux termes est souvent minime et contextuelle. Dans de nombreux cas, ils sont utilisés de manière interchangeable pour décrire les principes fondamentaux sur lesquels est édifiée une théorie ou un système de pensée.

Je suis d'accord: la discussion sur le sens d'un mot est vraiment d'une importance quasi nulle en mathématiques, ça sert à rien tout simplement
Et sa dernière phrase résume bien ce que tu dis.