Recherche fonction correspondant à une courbe

[ISONOE]

Bonjour,
J’ai un problème que je n’arrive pas à résoudre autrement que par itérations avec le solveur d’Excel.
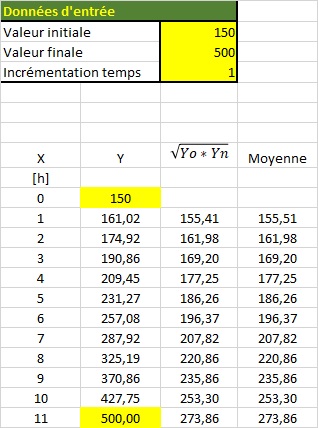
J’ai une courbe définie par un ensemble de points. Les points sont liés par les relations suivantes :
Racine carré (Yo x Yn) = moyenne des points de Yo à Yn
Avec :
(Xo ;Yo) le point initial de la courbe
(Xf ;Yf) le point final.
(Xn ;Yn) un point intermédiaire
(Xo ;Yo) et (Xf ;Yf) sont les données d’entrée
X et Y sont positifs.
Exemple :

Au point X=6 ; Y=257.08
racine carré de (257,08 x 150) = 196.37
moyenne des Y pour X variant de 0 à 6
Y = (150 + 161.02 + 174.92 + 190.86 + 209.45 + 231.27 + 257.08) / 7=196.37
La valeur de Y pour chaque points est obtenue par itération
Pensez-vous qu’il soit possible de définir une fonction correspondant à la courbe ?
Merci
-----

[gg0]

Bonjour.

Je suppose que les Xn sont connus, ou calculables avec les données initiales. Définir la suite des valeurs Yn, aucun problème, sauf cas particulier. Il s'agit de résoudre 10 équations à 10 inconnues, dans ton exemple, plus généralement f-1 équations à f-1 inconnues si f est bien l'indice du dernier terme (f=11 dans ton exemple). Plus une valeur imposée, celle de la moyenne finale, qui est donnée par les conditions initiales. Il faudra aussi préciser la précision demandée sur les valeurs approchées, car dans ton cas, la racine carrée de 150*500 n'est pas 273,86, mais 273,86127578...

A priori, vu qu'il y a des racines carrées, le résultat exact devrait être assez pénible à écrire, même si on se restreint à des valeurs positives. Par contre, la seule chose vraiment utile sera d'avoir la suite des valeurs Yn, le terme de fonction n'est pas très adapté. ni celui de "courbe" que tu as utilisé dans le titre.

Cordialement.

NB : Si j'ai un peu plus de temps, je regarderai le calcul exact dans ta situation.

[ISONOE]

Bonjour,
Oui les X sont connus. Ils représentent le temps. Je connais le temps nécessaire pour passer de la valeur Yo à Yf et je me fixe un pas de temps.
Mon problème est de formuler le passage de Yn à Yn+1 connaissant Yo, Yf, et le nombre de points pour passer de Yo à Yf et cela sans faire des itérations.
Une précision de l'ordre de 0.1% est suffisante.
Résoudre 10 équations à 10 inconnus en passant par les matrices je sais comment faire, mais pour ce problème je ne sais pas poser les équations.

Merci de s'intéresser à mon problème
Cordialement

[gg0]

A cause des racines carrées, les matrices ne suffiront probablement pas, le problème n'est pas linéaire.
En posant Zn pour la moyenne (et donc la racine carrée) à l'étape n, tu as
Zn²=Y0 Yn et Zn = (Y0+Y1+..+Yn)/(n+1)
Et tu as donc f équations de la forme Y0 Yn =[(Y0+Y1+..+Yn)/(n+1)]²

J'ai noté que dans ton tableau, il y a un net problème sur Z1 (2 valeurs différentes !).

Cordialement.

[A voir en vidéo sur Futura]

[GBZM]

Bonjour,

Et si au lieu de discrétiser tu passais au continu ?
Tu connais , et tu demandes que la fonction vérifie, pour tout ,

(ça dit que la moyenne géométrique des valeurs aux extrémités est égale à la moyenne arithmétique sur l'intervalle)

Tu fais le changement de fonction inconnue en posant , tu dérives par rapport à l'équation ci-dessus et ça te fait une équation différentielle assez facile à résoudre (je te laisse faire). Il convient bien sûr d'utiliser la condition donnée par la valeur en .

[GBZM]

Une erreur qui vient du fait que j'avais commencé par prendre pour simplifier. Il faut lire

[gg0]

Je viens de regarder de plus près ton problème, en fait il y a 11 équations, mais seulement 10 variables (de Y1 à Y10). Ce qui signifie que, en général, il n'y a pas de solution exacte. Ce qui explique le problème dans ton tableau. Ton solveur trouve des valeurs admissibles pour 10 équations sur 11, et laisse une erreur dans la onzième équation, celle qui concerne Y1.

Le calcul, même en n'imposant pas Yf=500 semble assez abominable, mon calculateur formel (Maple) n'avait rien trouvé au bout de 20 mn, il calculait toujours !

D'où vient ce problème ?

[GBZM]

Je répète que le problème continu se traite très facilement à la main !

[ISONOE]

La solution proposée par GBZM est séduisante mais mon niveau en mathématiques ne me permet pas de poursuivre son calcul pour l'exploiter et transcrire sur un tableur.

La solution que j'avais initialement c'était d'utiliser un solveur puis d'utiliser un outil permettant de trouver les coefficients de la courbe de tendance (polynomiale). mais cette solution n'est pas élégante et lourde à exploiter.

GBZM sans vouloir abuser de votre temps, pouvez-vous me communiquer une solution directement exploitable?

Merci à vous deux

[GBZM]

D'abord, peux-tu nous dire si ton problème est effectivement la discrétisation d'un phénomène continu ? D'où sort ta question ?
L'approche que je propose n'a de sens que si on est effectivement dans une situation continue, avec qui possède la propriété que la valeur moyenne de sur l'intervalle est égale à (la moyenne géométrique des valeurs aux extrémités de l'intervalle), pour tout . Une telle fonction est alors de la forme . Tu ajustes et avec deux valeurs de la fonction que tu imposes a priori. Par exemple pour et on obtient et .

[ISONOE]

Oui ce problème est bien un système continu. C'est la représentation de l'encrassement d'un filtre dans le temps. On part avec une perte de charge initiale jusqu'à une valeur qui nécessite son remplacement.
le niveau d'encrassement du filtre associé à une turbine à une incidence sur la consommation électrique.
Avec ta formule je vais pouvoir combiner plus facilement plusieurs étages de filtres et faire de l'optimisation énergétique...

Un grand merci.

[GBZM]

Avec plaisir,
La modélisation qui dit que l'encrassement moyen sur une période est égal à la moyenne géométrique de l'encrassement au début et à la fin reste un mystère pour moi.

[SULREN]

Bonjour,
Je n’ai pas du tout le niveau qui m’aurait permis d’intervenir dans cette discussion mais je l’ai suivie avec beaucoup d’intérêt. Merci à vous deux.

DANS LE CAS DU FILTRE :
Je commencerais par me dire :
-1) L’encrassement d’un filtre pendant une période de fonctionnement donnée est proportionnel au volume qui a traversé ce filtre, c’est-à-dire au débit moyen qui l’a traversé pendant cette période multiplié par le temps (ou bien écrire une intégrale).

-2) La perte de charge Delta P que crée un filtre est proportionnelle au carré du débit qui le traverse (mécanique des fluides) et à l'encrassement. Delta P = K * Q^2

-3) Le débit qui traverse le filtre diminue au fur et à mesure que l’encrassement augmente, car il est une fonction de la pression qui règne à l’entrée de l’étage d’aspiration de la turbine et que cette pression est égale à la pression atmosphérique – Delta P.

Ensuite j’essaierais d’écrire les équations correspondantes. Et là……

[ISONOE]

Bonjour,

La courbe d'encrassement est une donnée constructeur qui correspond à des essais et qui est propre à la technologie développée, tailles des particules... (je n'ai pas le choix que de retenir la donnée constructeur).

En ce qui concerne l'évolution des pertes de charge je suis d'accord avec SULREN (Loi de BERNOULLI).
Dans mon cas j'ai une action continue sur la vitesse de la turbine pour maintenir le débit constant (Loi de similitude RATEAU) afin de maintenir les performances du process....

[SULREN]

Bonjour,

@ISONOE:
La solution proposée par @GBZM répond à ta question et on peut donc considérer le sujet comme clôt.

Je fais juste ici (si la Modération le permet), part de ma réflexion sur ce problème de filtre de turbine, que je découvre et j’essaie d’expliquer par un raisonnement « technologique » pourquoi on constate la loi de variation de "y" que tu as indiquée dans ton tableur Excel.

La perte de charge "y" est égale à la perte de charge initiale plus celle résultant de l’encrassement (loi de Bernouilli)
Donc : y = 150 + E * Q^2 avec E étant l’encrassement du filtre.

Tu dis que :
- Dans le cas de cette turbine Rateau le débit est maintenu constant, donc qu’il ne varie pas en fonction de l’encrassement du filtre, contrairementau cas général des machines.
- L’encrassement du filtre n’est pas proportionnel au volume qui l’a traversé (comme je l’avais supposé dans mon premier post) mais qu’il faut tenir compte du diamètre des particules. On peut donc supposer que plus le filtre est encrassé plus il devient filtrant et retient des particules plus fines, donc plus sa vitesse d’encrassement augmente pour un volume traversant donné.

L’encrassement est donc proportionnel au volume (a*Q) qui passe et en PLUS à un facteur dépendant de son propre état.
Par simplification j’assimile ce facteur à un facteur proportionnel au temps et je le désigne par (b*t)

Donc l’encrassement E est l’intégrale ʃ (de t=0 à t=t) de la fonction : a*Q + b*t
Ce qui donne : E = a*Q*t + b/2*t^2

Donc l’expression initiale : y = 150 + E * Q^2
Devient : y = 150 + (a*Q*t + b/2*t^2) * Q^2 avec Q étant une constante
Donc "y" est de la forme :

y = 150 + A*t + B*t^2

En prenant A = 0,415 et B = 2,855 on trouve une loi de variation de « y » qui ressemble à celle donnée dans ton tableur.
(En affinant le facteur que j’avais simplifié en b*t et en le rendant fonction de E on trouverait la même loi).

NB : sur mes 12 machines de motoculture et autres, je penserai désormais à ce problème de taille de particules chaque fois que je vérifierai l’état de leur filtre.

[GBZM]

Je n'ai aucune compétence concernant l'encrassement des filtrss, mais je peux expliquer la résolution de l'équation

Comme je l'ai dit, on peut changer de fonction inconnue en posant . L'équation devient (en chassant aussi le dénominateur)

où j'ai posé . En dérivant on a l'équadiff

qui est une équation à variables séparables

qui s'intègre sans peine en

où est une constante d'intégration que l'on calcule en fixant , ce qui donne . On en tire

On se souvient que . C'est bien une fonction de la forme

[Biname]

Salut,
En théorie c'est lourd, en pratique c'est très simple, il s'agit de trouver une "régression", il étonnant que ce mot n'apparaisse pas dans cette conversation.

 Cliquez pour afficher

# https://stats.blue/Stats_Suite/polyn...alculator.html
Y introduire tes points, choisir le degré du polynôme souhaité et cliquer sur calculate.
Copie-colle ceci
Points donnés x :

0
1
2
3
4
5
6
7
8
9
10
11

Points donnés y :

150.00
161.02
174.92
190.86
209.45
231.27
257.08
287.92
325.19
370.86
427.75
500.00

Excel doit le faire? ainsi que des tas d'autres sites qui te proposeront d'autres types de régressions

Tu peux aussi poser cette question à ChatGPT ou a Bard ou à Bing
"Ecrire un code régression polynomiale de degré n avec python, plot et fonction
150, 161.02, 174.92, 190.86, 209.45, 231.27, 257.08, 287.92, 325.19, 370.86, 427.75, 500 avec x de 0 à 11"

Pour la régression polynomiale:
tu écris y = ax³ + bx² + cx + d
tu utilises 4 de tes points(x_i, y_i) bien choisis pour calculer 4 équations linéaires à 4 inconnues
yi = ax_i³ + bx_i² + cx_i + d
Ce système va te permettre de calculer les a,b,c et d de ta fonction
Un boulot d'enfer à la main que va faire le site avec deux copié-collé et deux clics, en plus, il te tracera la fonction et tes points, calculera des paramètres permettant de vérifier la qualité de ta régression.

Avec 10 points, tu peux écrire un polynôme de degré 9 et 10 équ à 10 inc

Un bon PC résout 5000 équations linéaires à 5000 inconnues en 1 seconde.

Biname

[SULREN]

Bonsoir,

@GBMZ :
Entendons nous bien :
Etant donné mon niveau ridicule en mathématiques, j’ose à peine mettre les pieds sur ce forum. Il ne me viendrait donc pas à l’esprit d’aller contester ce que les autres membres écrivent, et encore bien moins quand il s’agit de membres de haut niveau dans ce domaine.
J’ai bien écrit d’entrée que @ISONOE était venu chercher une équation et qu’il avait eu sa réponse.
(Je sais chercher les régressions pour mes propres besoin, mais dans le cas présent je n’ai même pas essayé).

Mais comme cette discussion a éveillé ma curiosité sur la dynamique de colmatage des filtres, sujet que je côtoie au quotidien mais que je n’ai jamais cherché à modéliser, j’ai voulu saisir cette occasion pour en parler avec @ISONOE et exploiter les informations qu’il avait données :
- La perte de charge « y » dans le filtre part de la valeur initiale150 lorsque le filtre est neuf et augmente en fonction de l’encrassement pour devenir 500 au temps t=11
- Cette perte de charge est bien de type y= E *Q^2 avec E encrassement qui fait obstacle à l’écoulement
- Le débit Q reste constant, malgré l’encrassement (ce qui simplifie la modélisation).
- MAIS la vitesse d’encrassement n’est pas seulement proportionnelle au débit (comme on le considère habituellement). Elle augmente avec l’importance de l’encrassement, à cause de la capacité augmentée de rétention des particules fines.

Pour éviter de résoudre l’équation implicite : E dépend de E (même si j’en ai l’habitude en mécanique des fluides : équation de Colebrook White, par exemple) j’ai simplifié en disant que cette vitesse augmentait avec le temps.

Et malgré cette approximation j’ai eu la surprise de voir que la forme de la courbe à laquelle j’aboutissais ressemblait à celle de ISONOE (mais bien moins que ne le fait celle de @GBMZ).
TABLEAU CI-JOINT
J’ai cru bon en parler ici, mais peut être à tort. Sans intervenir désormais ici, je vais continuer à approfondir l’équation implicite E dépend de E pour essayer de peaufiner la modélisation du colmatage,…..et je vais chercher des thèses sur la Dynamique du Colmatage des Filtres.

NB : Histoire vraie, pour le fun :
Suite à une discussion du même genre il y a 20 ans, sur la dynamique d’échauffement au cœur d’une meule de foin consécutive à une récolte de foin insuffisamment sec (sujet que le fils de paysan que je suis connais) j’ai fini par bien comprendre en lisant une thèse : sur la Déshydratation des Fourrages.

[GBZM]

J'ai dû mal recopier les résultats que j'avais fait calculer pour a et b.

[Biname]

Salut,
Avec les données ci dessus, voici 12 images png (une par degré) zippées comparant les régressions polynomiales de degré 0 à 11 avec y = a/(b-x)² pour a = 88229 et b = 24.321

Chaque image comprend 2 graphiques, un donnant les deux régressions et les points, l'autre les résidus des deux régressions.

Un exemple où les deux régressions se valent:

 Cliquez pour afficher

regression_plot_degre_02.png

Un fichier contenant les 12 images png
12_plots.zip
La précision des données font douter qu'il s'agit de mesures ?
Biname

[Biname]

Salut,

Avec les données ci dessus, voici 12 images png (une par degré) zippées comparant les régressions polynomiales de degré 0 à 11 avec y = a/(b-x)² pour a = 88229 et b = 24.321 ...

Dans l'équation écrite sur les png, les coefficients des termes sont inversés et il y a un pb de signe, les graphiques eux sont exacts.
Voici une version corrigée. Promis, il n'y en aura pas d'autres
Exemple degré 11, résidus max e-10 (log plot abs(résidus) et coef termes en notation scientifique)

 Cliquez pour afficher

regression_plot_degre_11_cor.png

Et le zip corrigé contenant les 11 cas :12plots_cor.zip
En faisant défiler les images 'degré croissant', on voit la qualité de la régression s'améliorer.
Biname

[SULREN]

Bonjour à tous,

@Biname :
Salut. J’ai juste regardé les 11 courbes ce matin avant d’aller faire mes courses, sans examiner les expressions et sans remarquer les erreurs qu’elles comportaient.
Très beau travail ! Bravo ! Je suis bluffé par la puissance des outils actuels pour trouver les régressions.
L’ami @Isonoe a l’embarras du choix, mais l’équation que lui a gentiment fournie @GBZM avait déjà une précision suffisante pour lui permettre de faire ce qu’il a dit au post#11, à savoir : « Avec ta formule je vais pouvoir combiner plus facilement plusieurs étages de filtres et faire de l'optimisation énergétique.»

La constructeur de la turbine donne un profil de courbe de « y » entre le point de départ à 150 et d’arrivée à 500, qui résulte de mesures et/ou de calculs, mais qui correspondent certainement à la réalité de sa machine.
Pourquoi ne donne t’il pas aussi directement aux utilisateurs les éléments leur permettant de faire de l’optimisation énergétique ?

En ce qui me concerne je n’ai pas du tout cherché à trouver une régression de la courbe mais à déterminer moi-même le profil de cette courbe entre les points extrêmes 150 et 500, en modélisant l’encrassement du filtre et sa perte de charge, sur la base de mes connaissances dans ce domaine.
J’ai voulu profiter de ce bel exemple de filtre donné par @Isonoe pour m’entraîner à cet exercice.
C’est par pure curiosité, car en pratique je n’en ai nullement besoin.

Je constate que mes connaissances sont notoirement insuffisantes, puisque la courbe que j’ai trouvée s’écarte de la courbe indiquée.
Je trouverai bien un thésard qui a déjà expliqué tout cela.

[SULREN]

Re,

@Biname:
Finalement, il n'était pas si nul que cela mon polynôme de degré 2, par rapport à ta régression polynomiale de degré 2, sachant qu'il n'était pas, lui, une régression cherchant à imiter au mieux la courbe source (celle de @ISONOE), mais qu'il résultait de la modélisation du phénomène d'encrassement, ....certes en connaissant les deux points extrêmes visés: 150 et 500.

[GBZM]

Les fournis par ISONOE ne sont pas des résultats d'expérience. Ce sont des valeurs calculées à partir

1. de la valeur initiale pour
2. de la valeur finale pour
3. de la condition (*) : la valeur moyenne sur tout intervalle est égale à la moyenne géométrique des valeurs aux bornes de l'intervalle.

ISONOE discrétise cette condition en imposant où est la valeur en pour . Je discrétiserais plutôt le calcul de la valeur moyenne sur l'intevalle pour par (c'est la méthode des trapèzes, qui donne une meilleure approximation)
J'ai démontré qu'une fonction du temps qui vérifie la condition (*) est de la forme . Avec la valeur 150 en et 500 en , on obtient et (j'avais fait une coquille en recopiant le précédemment).
À mon avis, faire une régression sur les valeurs fournies par ISONOE ne présente aucun intérêt vu que ces valeurs ne sont pas des résultats d'expérience, mais viennent d'un calcul fait à partir d'une discrétisation du problème qui est loin d'être optimale !

Il reste une question à laquelle je n'ai eu aucune réponse : d'où vient cette condition (*) ?? ISONOE ne l'a tout de même pas inventée au hasard ! Tombe-t-elle du ciel ? Résulte-t-elle d'une étude théorique basée sur une modélisation des phénomènes ? Vient-elle d'une documentation du constructeur ?
J'aimerais bien qu'ISONOE réponde là-dessus.

[GBZM]

Deux petites remarques :
1) La condition (*) peut se formuler ainsi : "La valeur à l'instant est proportionnelle au carré de la valeur moyenne sur l'intervalle de temps [0,t]." Ça n'explique pas plus cette condition, pour laquelle on attend une réponse d'ISONOE.
2) Il est facile de vérifier pour une fonction de la forme la condition que la valeur moyenne sur un intervalle (ne contenant pas ) est égale à la moyenne géométrique des valeurs aux extrémités de l'intervalle. Prenons par exemple . Alors et

[SULREN]

Bonjour,

En effet, même si ces valeurs ont peut-être été inspirées par des relevés sur machine, les valeurs qui nous ont été présentées suivent une loi purement mathématique, dont l’allure générale est de type y=a*t^(voisin de2), ce qui correspond à ce qu’on trouve comme perte de charge en fonction du temps aux bornes d’un filtre .
Le dernier cas que j’avais observé était de type y = a * t^2,15
Seul @ISONOE pourra nous dire d’où il l’a tirée.

En attendant, je me permets de soumettre mon approche de la modélisation.
(Post à supprimer sans hésitation, si jugé inopportun par @GBZM ou plein d’erreurs de raisonnement).

En supposant le diamètre constant, l’accélération de la pesanteur constante, etc :
y = K *Q^2
y : perte de charge
K : coefficient de perte de charges
Q : débit massique

K = K0 + E(t) avec :
K0 : coefficient de perte de charge initial à t=0 lorsque le filtre est neuf
E(t) : coefficient de perte de charge additionnel, dû à l’encrassement du filtre et augmentant donc dans le temps

E(t) = ʃ ( Q * mi * FR(E) sur l’intervalle {0,t}
C’est-à-dire (comme je ne sais pas écrire en Latex ), l’intégrale de (Q * mi * FR(E)) sur {0,t}
Q : débit, donné comme constant dans le cas présent
mi : Masse d’impuretés par unité de volume, supposée constante dans le temps dans le cas présent
FR(E) : facteur de rétention du filtre dans l’état d’encrassement dans lequel il est à l'instant t.

On écrit :
FR(E) = FR0 + f(E)
FR0 : facteur de rétention des impuretés par le filtre propre, quand E=0 ; Par exemple : FR0= 90/100
f(E) : augmentation du facteur de rétention du filtre quand il est encrassé, parce qu’il piège de mieux en mieux les particules, en particulier les fines.

Donc :
E(t) = ʃ (Q * mi * FR0) + ʃ (Q * mi * f(E)) On tombe sur une formule implicite : E dépend de E
E(t) = Q * mi * FR0 * t + Q * mi * Fonction?(de t)

Donc la perte de charge s’écrit :
Y = [K0 + E(t)] * Q^2
Et on sait que K0 * Q^2 = 150
On dit que : Q * mi * FR0 * Q^2 = A étant donné que Q, mi, FR0, sont constants
On dit que : Q * mi * Q^2 = B

Y = 150+ A*t + B * Fonction?(de t)

Je ne sais pas trouver cette Fonction?(de t) qui est une fonction de degré au moins égal à 2
On est dans un cas d’équation implicite. Je l’avais déjà dit dans un post précédent.

[GBZM]

Bel effort, mais il n'y a pas que les fonctions pouissances dans la vie ...
Dommage qu'ISINOE ne nous dise pas où il a péché sa condition (*).

[ISONOE]

Tout d'abord je suis très surpris de constater que la discussion s'est poursuivi alors que je la considérai close avec la réponse donnée par GBZM.
GBZM a parfaitement compris mon problème. Les valeurs du tableau ne sont pas le résultat de mesures mais viennent d'un calcul fait à partir d'une discrétisation du problème loin d'être optimale!
En ce qui concerne la condition (*) : la valeur moyenne sur tout intervalle est égale à la moyenne géométrique des valeurs aux bornes de l'intervalle.
Elle est donnée par le constructeur. Cette condition n'est pas forcément rigoureuse mais elle donne des résultats proche de la réalité et facilement modélisable comme l'a démontré GBZM, où à partir des conditions initiales et finales, on a le comportement du filtre (modélisation plus proche qu'une fonction exponentielle ou une équation du second degré) et facilement exploitable.

@GBZM: J'ai un petit problème d'affichage. Les formules contenues dans vos discussions apparaissent sous forme de pictogramme "image" et donc illisibles et la démonstration de la formule m'intéresse. C'est ma première discussion et je ne maîtrise pas l'outil!
Encore merci, la formule est facile à exploiter et répond parfaitement à mon besoin quelque soit les conditions aux limites.

[GBZM]

Désolé, mais c'est un bug du forum qui fait que les formules LaTeX n'apparaissent plus. Espérons que cela sera réglé bientôt !

[gg0]

Bonjour.

On peut retrouver les formules en langage natif avec "Répondre avec citation"
Cordialement.