Courbe=Fonction?

[Houdini195]

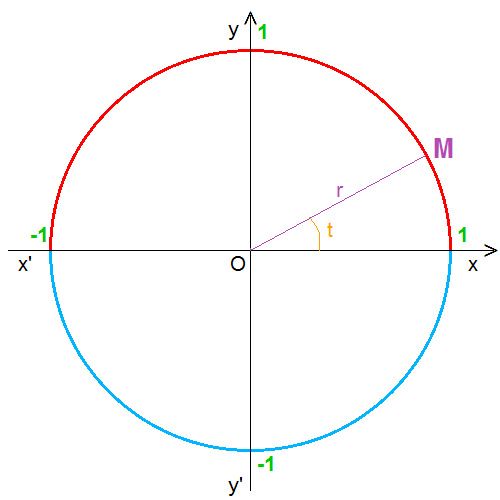
Bonjour à tous,
Je ne sais pas si mon message est posté dans la bonne section et si ce n'est pas le cas je m'en excuse d'avance. J'ai une question de pure curiosité mais peut-être celle-ci est stupide car je n'ai certainement pas les notions pour pouvoir aborder ce sujet n'étant qu'en première. A tout hasard je la pose tout de même:
Est-ce qu'à toute courbe est associée une fonction?
Même la plus tordue de toute les courbes que l'on pourra dessiner était-elle théoriquement représentative d'une fonction?
Quand j'ai posé cette question à ma prof elle m'a montré les fonctions du type r= et je me suis donc rendu compte que j'avais si peu de connaissances que peut-être ma question était dénuée de sens mais si quelqu'un pense pouvoir me donner une sorte de réponse qui me soit abordable ce serait très sympa.
Merci d'avance
-----

[Médiat]

Bonjour,

Oui à toute courbe est associée une fonction, mais pas forcément une fonction de IR dans IR, et pas forcément une fonction exprimable sous les formes que vous connaissez (ou d'autres)

[Houdini195]

Merci beaucoup!

[gg0]

Bonjour.

Pour le niveau de seconde :

Dans un repère donné, les courbes de fonctions numériques ont la propriété que pour une abscisse donnée, il y a 0 ou 1 point de la courbe (puisque l'abscisse est un antécédent qui a une seule image, ou n'est pas un antécédent). Donc toute courbe qui a plusieurs points de même abscisse n'est pas la courbe d'une fonction numérique. Par exemple un cercle n'est jamais la courbe d'une fonction numérique.

Cordialement.

[A voir en vidéo sur Futura]

[Houdini195]

D'accord merci. Donc une courbe qui aurait plusieurs points d'intersection avec une droite parallèle à l'axe des abscisses serait représentative d'une fonction non numérique?

[gg0]

Heu ... c'est difficile de dire "représentative". Il vaut mieux te contenter, pour l'instant, de connaître les notions de courbes représentatives de fonctions (déjà très riche) et d'équations de courbes (il y a plusieurs notions). Et de dire "une courbe qui aurait plusieurs points d'intersection avec une droite parallèle à l'axe des abscisses ne serait pas la courbe représentative d'une fonction numérique".

[gg0]

Tu peux explorer les façons de définir les courbes, en piochant sur Internet avec les mots "courbes paramétriques", "courbes en polaire". Tu auras déjà de quoi penser

[Houdini195]

Merci du conseil, je vais m'occuper avec ça ces prochains jours alors

[Opabinia]

Bonjour,

Pour prendre l'exemple du cercle de rayon 1 centré à l'origine (O)

a) la courbe entière correspond à l'ensemble des points du plan séparés de l'origine par une distance égale au rayon (OM = R = 1),
et dont les coordonnées vérifient l'équation cartésienne: x² + y² = R² (= 1);
b) le demi-cercle supérieur (y ≥ 0 , tracé en rouge) est le graphe des variations de la fonction y = F₁(x) = (1 - x²)^1/2 ,
le demi-cercle inférieur (y ≤ 0 , tracé en bleu) celui de la fonction y = F₂(x) = -(1 - x²)^1/2 ;
c) le cercle est la courbe fermée présentant l'équation polaire la plus simple: r = R (r correspondant par définition à OM);
d) il est aussi défini par les équations paramétriques: x = R.Cos(t) , y = R.Sin(t) .

Voir ici, par exemple.

Les équations paramétriques permettent de définir les courbes les plus variées.
Tu en trouveras de nombreux exemples sur le même site.

[Houdini195]

Ok! Ça a l'air vraiment intéressant je vais lire vos liens et je vous tiens au courant