Bonjour
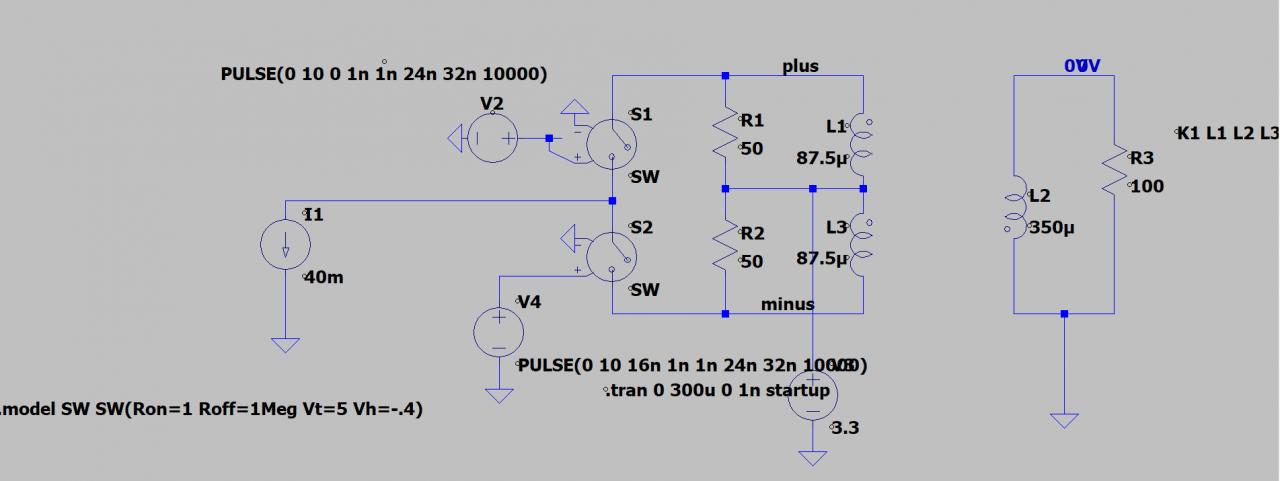
L'ethernet 100 Base-TX s'appuie sur un émetteur dont une des architectures possible est le current mode logic dont voici un schéma équivalent.
1. Le schéma est réalisé sous LTSPICE, mais je n'arrive pas à retrouver le résultat par le calcul. Pourriez-vous m'aider?
J'ai un système d'équation de la forme:
I0 = i1(Lp/(4R) +1)+ i2 Lp/(4R) + i3 Lp/(2R)
0 = i1 Lp/(4R) + i2 (Lp/(4R) + 1) + i3 Lp/(2R)
0 = i1 Lp/(4R) + i2 Lp/(4R) + i3 (Lp/(2R) +1)
I0 = 40 mA
L = 350 µH
R = 50 Ohm
J'obtiens une équation différentielle pour i1 de la forme
I0(1+3Lp/(4R)) = i1(1 + Lp/R)
A partir de là, si je prends I0 = constante, la solution est de la forme
i1(t) = I0(1 - exp(-t/taux)) avec taux = L/R, ce qui ne colle pas avec la simulation.
Si je prends I0(t) = I0 x u(t), u(t) étant la fonction échelon, je ne sais pas trop comment me sortir du I0 x 3L/(4R) x dirac(t)
2. J'ai essayé de simplifier le schéma en partant d'une condition initiale
i(L1,t=0) = 20mA
i(L2,t=0) = -20mA
i(S1,t) = -40mA
i(S2,t) = 0mA
La simulation donne quelque chose comme
i1(t) = 40mA(1- 1/4 x exp(-t/taux))
i3(t) = -10mA(1-1/4 x exp(-t/taux))
i2(t) = 10mA(1-1/4 x exp(-t/taux))
taux = L/R
La mise en équation précédente me semble applicable et correcte, mais là encore, je ne trouve pas la solution. Est-ce que ce cas vous semble plus simple à traiter?
Merci pour votre aide!
Etienne
-----