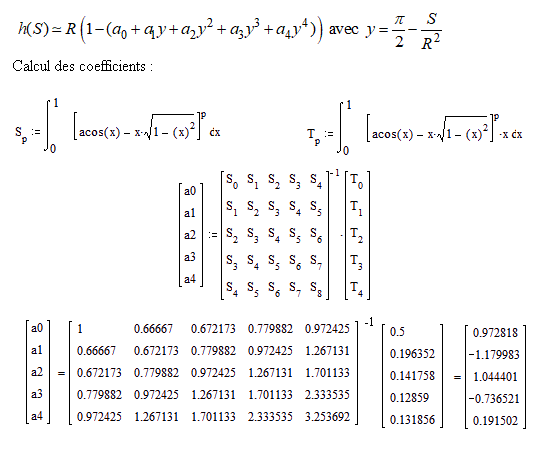Inverser cette fonction

[Jean.Marc]

Bonjour,
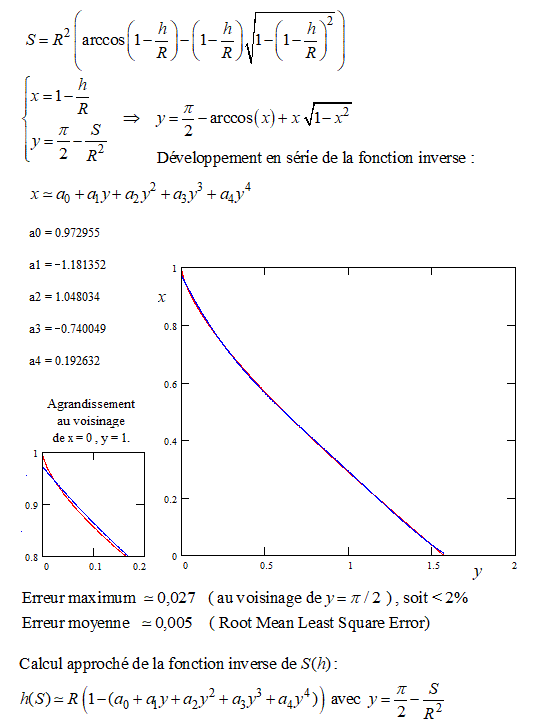
J'ai péniblement défini cette fonction:



où h est la variable et R un paramètre.

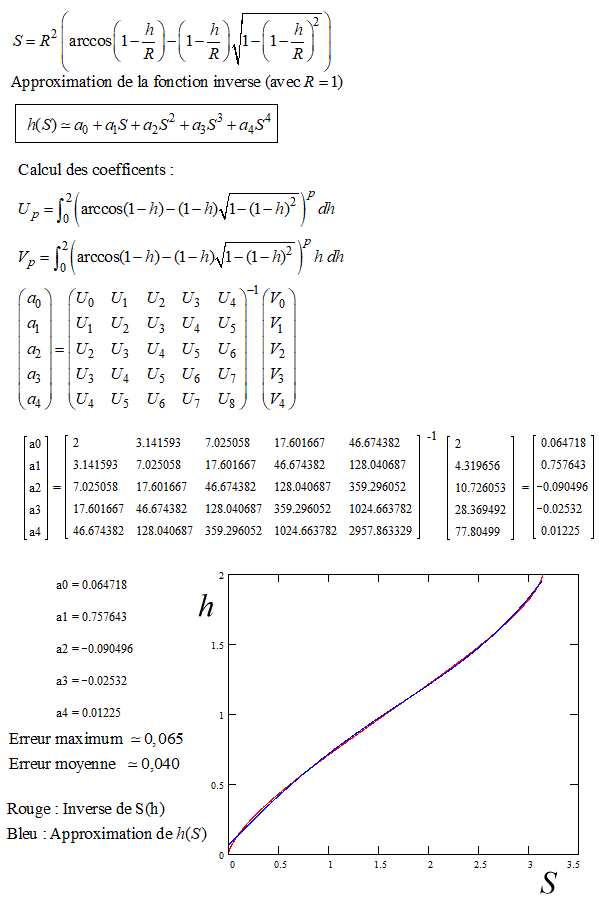
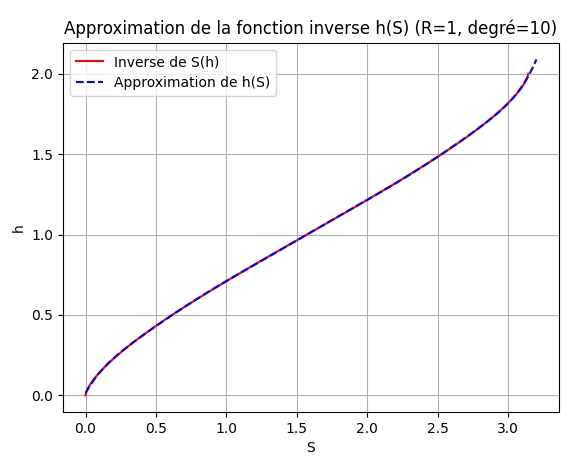
et maintenant, je voudrais la fonction réciproque :

h = f(S) où R est un paramètre.

Et là, mon niveau de maths ne me permet pas d'y arriver. Qui peut m'aider?
Merci.
-----

[gg0]

Bonjour.

Je ne crois pas qu'il existe de calcul algébrique permettant d'exprimer la fonction réciproque.
On peut par contre obtenir une assez bonne approximation de la fonction pour h pas trop proche de 0 ou de 2R :

qui permet d'inverser avec une bonne approximation.

Cordialement.

[Jean.Marc]

Merci.

Je joins la courbe de la fonction originale (en rouge) et celle de l'erreur de la fonction approchée (en bleu). Malheureusement, l'erreur est trop grande pour mon application.
Il me reste la solution de faire une table de valeurs et une fonction de recherche dans Excel...

[gg0]

Tu as pris ici R=0,8. Donc l'approximation est "bonne" aux alentours de 0,4. C'est bien ce qu'on voit.
Si R est fixe, une résolution de y=f(x) pour un certain nombre de valeurs de y entre 0 et Pi R² puis l'utilisation d'interpolation linéaire devrait donner un bon résultat. Tu peux aussi utiliser l'approximation pour y entre disons R² et 2R² (à toi de voir ce qui convient), mais comme la courbe est quasi linéaire, l'interpolation fonctionne parfaitement, donc ça complique. Suivant tes capacités informatiques, tu prends des valeurs régulièrement espacées (plus simple), ou tu prends plus de valeurs au voisinage de 0 et à celui de Pi R².

Cordialement

[A voir en vidéo sur Futura]

[JJacquelin]

Bonjour,
Avec un changement de variables qui facilite (un peu) le calcul d'une série limitée :

[JJacquelin]

La courbe rouge est la symétrique (par rapport à la diagonale) de la courbe y(x) selon la fonction S(h) donnée.
La courbe bleue est tracée par le calcul approché de x(y) selon le développement limité.
Les deux courbes sont presque superposées.

Erreur typographique à corriger sur la figure : L'agrandissement est bien évidemment au voisinage de x=1 , y=0.

[JJacquelin]

Correction : L'erreur maximum est bien évidemment au voisinage de y=0 et non pas au voisinage de y=pi/2.
Il y a aussi une erreur typographique sur la figure : L'agrandissement est au voisinage de x=1 et y=0.

[Biname]

Salut,
Ici une régression polynomiale de degré 3 sur les valeurs de S(h) pour trouver le polynôme
R = 1

 Cliquez pour afficher

Poly_1.jpg
Residus.jpg

[erff]

Bonsoir,

Une approche manuelle just for fun.

Avec les bons changements de variables et un peu de trigo, l'équation à résoudre revient à : , où x=1-h/R et où x€[-1,1], et A=S/R^2.
Sachant que c'est un signe - si x>0 et et un signe + sinon.

Soit alors
Par ailleurs, un DL en 0 montre qu'une solution approchée (1ère itération) serait donnée par

La 1ère itération de Newton-Raphson (dans le cas x > 0 càd h<R) permet d'exprimer une solution approchée par :


Voici un graphique qui permet de comparer la "vraie" solution (solveur numérique) et l'approximation proposée pour plusieurs valeurs possibles du paramètre A=S/R^2 (axe des abscisses). On commet moins de 1.2% d'erreur pour A€]0,2.25]. Et pour info l'approximation devient mauvaise à partir d'un certain A : elle donne ~10% d'erreur à partir de A=3.



Bonne soirée

[JJacquelin]

En complément à ma réponse #5 du 20 mai 2024.
Les coefficients du polynôme sont calculables de la façon suivante.
Cet exemple est pour un polynôme de degré 4.
Bien entendu, on pourrait choisir un degré différent, selon la précision d'ajustement que l'on souhaite.

[JJacquelin]

METHODE PLUS DIRECTE :

(Oublier mes messages précédents)

L'exemple numérique est fait avec un polynôme de degré 4. On voit aisément comment faire de même avec un polynôme de degré différent (Selon la précision de l'ajustement que l'on souhaite).

[Biname]

Salut,
J'ai passé ton image à 4o, il m'a sorti le code python de ton exemple en 10 secondes, R et degré du polynôme variables(dans mon exemple, il utilisait curve_fit de scipy).

 Cliquez pour afficher

# solution JJACQUELIN 4o(jpg de tex)
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from scipy.integrate import quad

# Définir les symboles
h = sp.Symbol('h')
R = 1  # On fixe R = 1

# Définir l'expression de S(h) pour R = 1
S_expr = sp.acos(1 - h) - (1 - h) * sp.sqrt(1 - (1 - h)**2)
S_func = sp.lambdify(h, S_expr, 'numpy')

# Calculer les U_p et V_p
def U_p(p):
    integrand = lambda h: (S_func(h))**p
    return quad(integrand, 0, 2)[0]

def V_p(p):
    integrand = lambda h: h * (S_func(h))**p
    return quad(integrand, 0, 2)[0]

# Construire les matrices U et V
degree = 4
U = np.zeros((degree+1, degree+1))
V = np.zeros(degree+1)

for i in range(degree+1):
    V[i] = V_p(i)
    for j in range(degree+1):
        U[i, j] = U_p(i + j)

# Résoudre le système linéaire pour trouver les coefficients
a = np.linalg.solve(U, V)

# Afficher les coefficients
for i in range(degree+1):
    print(f'a{i} = {a[i]}')

# Définir la fonction polynomiale h(S)
def h_approx(S, a):
    return sum(a[i] * S**i for i in range(len(a)))

# Générer des valeurs de S pour tracer h(S)
S_vals = np.linspace(0, 3.2, 100)
h_vals_approx = h_approx(S_vals, a)

# Tracer h(S) approximé et les données réelles
h_vals_real = np.linspace(0, 2, 100)
S_vals_real = S_func(h_vals_real)

plt.plot(S_vals_real, h_vals_real, 'r-', label='Inverse de S(h)')
plt.plot(S_vals, h_vals_approx, 'b--', label='Approximation de h(S)')
plt.xlabel('S')
plt.ylabel('h')
plt.legend()
plt.title(f'Approximation de la fonction inverse h(S) (R={R}, degré={degree})')
plt.grid(True)
plt.show()

# Calculer les résidus
h_pred = h_approx(S_vals_real, a)
residuals = h_vals_real - h_pred

# Afficher les résidus
plt.figure()
plt.plot(S_vals_real, residuals, 'o', label='Résidus')
plt.axhline(y=0, color='r', linestyle='-')
plt.xlabel('S')
plt.ylabel('h - h_pred')
plt.legend()
plt.grid(True)
plt.title('Résidus de la régression polynomiale')
plt.show()

[JJacquelin]

@ Biname,
Très bien. Avec cela Jean.Marc devrait être satisfait.