Intégrale curviligne le long d'un chemin exercice

[CobeLegrand]

Bonjour je viens de commencer les intégrales curvilignes et je voudrais savoir si ma méthode pour calculer des intégrales curviligne le long d'un chemin est la bonne:


Ici avec le 1 :

γ(t) = (2t, t), t ∈ [0,1]
donc xγ(t) = 2t
γ' = 2 et IIγII = racine(5)
1
donc ∫ xdγ= ∫ racine(5).2t entre 0 et 1
= racine(5) . ∫2t entre 0 et 1 =racine(5)

Merci pour votre aide.
-----

[gg0]

Bonjour.

Tu as appliqué la méthode et trouvé un résultat. Donc tu sais faire. Fais le deuxième ...

Cordialement.

[CobeLegrand]

D'accord donc mon résultat est le bon ?
Donc pour le deuxième ducoup ça donnerai :


γ(t) = (cos(t), sin(t)), t ∈ [0,π/2]
donc yγ(t) = sin(t)
γ' = -sin(t) et IIγII = 1
cos(t)
donc ∫ ydγ= ∫ 1.sint(t) entre 0 et π/2
= ∫ sin(t) entre 0 et π/2 = 1

[gg0]

Bonjour.

J'ai interprété ce que tu écris au message #1, considérant que ce que je ne comprenais pas était des fautes de frappe. Ici, je n'en suis plus du tout sûr, en particulier la répétition de IIγII qui pose problème; sans compter la proximité typographique entre γ et y !! Le premier résultat était-il correct par hasard ??
Quelle est la formule que tu utilises ? Pour éviter les ennuis, appelle G la courbe (ici G(t) =(2t,t) puis G(t)=(cos(t),sin(t)), G correspond au Gamma majuscule grec).

Cordialement.

[A voir en vidéo sur Futura]

[CobeLegrand]

"IIγII" C'est la norme.

Avec G = γ
on a G(t) = (2t,t) , t ∈ [2t,t]
on a donc G' = 2 d'ou norme(G) = racine( 2^2 +1^2) = √5
1
Ensuite, ∫ xdG = ∫ 2t.√5 dt = √5.∫ 2t dt = √5.[t^2] le tout le long de 0 et 1 = √5

Pour le 2 :

G(t)=(cos(t),sin(t)) , t ∈ [0;π/2]
donc G' = -sint(t) donc norme(G) = racine(-sin^2(t) + cos^2(t)) = √1 = 1
cos(t)

∫ ydG = ∫ sin(t) .dt = [-cos(t)] le tout entre 0 et π/2 = 1

[gg0]

Non, ça ne va pas :

"on a G(t) = (2t,t) , t ∈ [2t,t]
on a donc G' = 2" Non, G'(t)=(2,1). La dérivation se fait composante par composante
"d'où norme(G) = racine( 2^2 +1^2) = √5" Non, ce n'est pas ||G|| qui vaut racine((2t)^2+t^2) = |t|racine(5)

Tu n'as pas donné la formule de ton cours. Je ne vais pas plus loin. Tu as une formule à utiliser, tu es en train de faire autre chose (imiter sans comprendre un exemple mal copié ???), tu perds ton temps.

[CobeLegrand]

Dans le cours j'ai uniquement ça : Capture d'écran 2024-03-08 150329.png
Avec un exemple.

Mais donc je fait pour reprendre le 1:
Capture d'écran 2024-03-08 153012.png

[gg0]

OK.

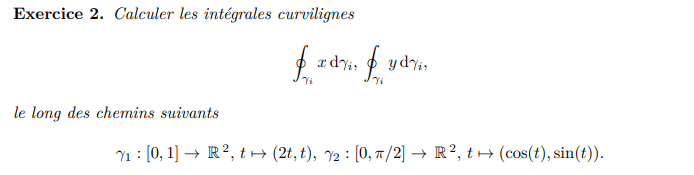
Ce qui compte, c'est d'appliquer la formule. Dans la formule c'est la norme euclidienne de , donc c'est ce que tu dois appliquer.
Il n'y a pas ce dans ton deuxième document, seulement un ||y|| qui n'a rien à voir. Et ensuite un ||(1,3)|| dont on ne sait pas d'où il sort, et qui vaut . Mais miraculeusement, il devient et le calcul redevient juste.
Je m'interroge sur le pourquoi de ce résultat juste avec un calcul systématiquement faux.Aurais-tu eu ça comme exemple, mais copié de travers ???

Bon, c'est ton exercice, c'est à toi de le faire : appliquer la formule. Tu as donc besoin de trouver
* combien vaut , donc en premier lieu identifier , puis trouver.
* déterminer , qui est un vecteur (un couple de réels), puis .
* remplacer dans la formule puis calculer l'intégrale.

Fais ça pour ...

[gg0]

Par exemple, avec et la première intégrale curviligne :
* (projection sur la première composante) donc
* donc
* l'intégrale est donc