Pi et fonctions hypergéométriques
Discussions similaires
-
Par ATdevice dans le forum Programmation et langages, Algorithmique
Réponses: 9
Dernier message: 05/08/2023, 19h40
-
Par invite248d9253 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 03/03/2013, 12h29
-
Par invite1bcc2991 dans le forum Mathématiques du supérieur
Réponses: 6
Dernier message: 04/01/2013, 13h04
-
Par invite46e41aed dans le forum Mathématiques du supérieur
Réponses: 3
Dernier message: 21/06/2012, 21h40
-
Par invitea87a1dd7 dans le forum Mathématiques du supérieur
Réponses: 6
Dernier message: 01/04/2007, 22h55





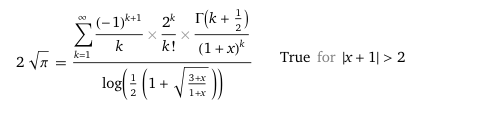

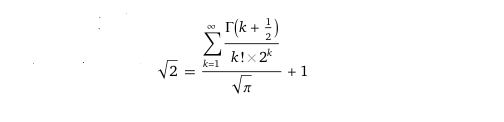
 , le
, le 