[Fonctions] Les fonctions égales à leur réciproque

[Aenonis]

Bonjour,

J'ai recherché, en son temps, la liste de toutes les fonctions égales à leur réciproques.

Mais, d'abord, définissons ce qu'est une "fonction égale à sa réciproque".

est une fonction égale à sa réciproque si , c'est à dire que leur graphique est symétrique à la fonction identique

On serait tenté de dire qu'il n'en existe qu'une: la bête fonction identique ainsi qu'une toute petite infinité: les fonctions du type avec .

Si on regarde la définition stricte, j'aurai pu m'arrêter là parce que, d'après moi, il n'en n'existait pas d'autres (cela demande vérification).

Mais en faisant des recherches, j'ai découvert le théorème suivant: (que je vais démontrer par après)
Si est égale à sa réciproque, alors est aussi égale à sa réciproque.
Démonstration:
Nous savons, par définition, que .
Prenons la composée de (que je nommerai par la suite) sur elle-même, il faut qu'elle soit égale à la fonction identique () afin de vérifier le théorème.
La composée demandée est la suivante: , en simplifiant, nous obtenons ceci:
Vu que , on peut encore simplifier: , ce qui nous amène à . Je terminerai ma démonstration par l'ultime .

Normalement, ce théorème nous assurerai, par construction successives, une infinité de fonctions répondant à la définition. Mais n'étant pas un matheux convaincu (je l'étais avant mais j'ai bifurqué dans l'informatique où je crée des programmes qui traitent de problèmes mathématiques, donc tout se tient ), je ne suis pas sûr de la rigoureusité de cette démonstration vu qu'en appliquant le théorème avec une fonction répondant à la définition de son égalité avec sa réciproque et une fonction quelconque (vu que je n'ai rien précisé pour dans le théorème), j'obtiens des fonctions qui ne satisfont pas la définition, en tout cas pas sur tout leur domaine.

En effet, en appliquant le théorème sur et avec et , je calcule d'abord qui vaut dans notre cas et donc, en calculant la fonction résultante , on obtient , ce qui devrait, avec le théorème être une fonction qui vérifie la définition. Pour donner une idée, fixons et : et , ce qui veut dire que la fonction résultante est: , ce qui n'est qu'autre que l'équation du demi-cercle centré en de rayon .

Arrêtez-moi si je me trompe, cette fonction ne vérifie pas tout à fait la symétrie sur , en effet, elle vérifie la définition sur la symétrie sur

Pire encore, si on rapplique le théorème sur le demi-cercle ainsi formé, on tombera sur une fonction qui est symétrique uniquement sur des parties de son domaine, ce qui peut vite devenir problématique si on applique le théorème disons une dizaine de fois, on risque de se retrouver avec des fonctions casi-quelconques (dont le domaine de "symétrie" se rétrécira à chaque fois), donc qui ne vérifie plus la dite définition.

Exemple pour illustrer ce soucis: on part toujours de avec , on applique le théorème avec , on obtient une nouvelle fonction , on rapplique le théorème sur cette fonction construite avec , nous obtenons donc la fonction suivante (que nous allons étudier par la suite et que nous nommerons pour plus de facilité): . J'ai calculé le domaine de symétrie pour cette fonction: , pour nous donner une idée du résultat, on va fixer , ce qui donne la fonction suivante: et le domaine de symétrie suivant: .

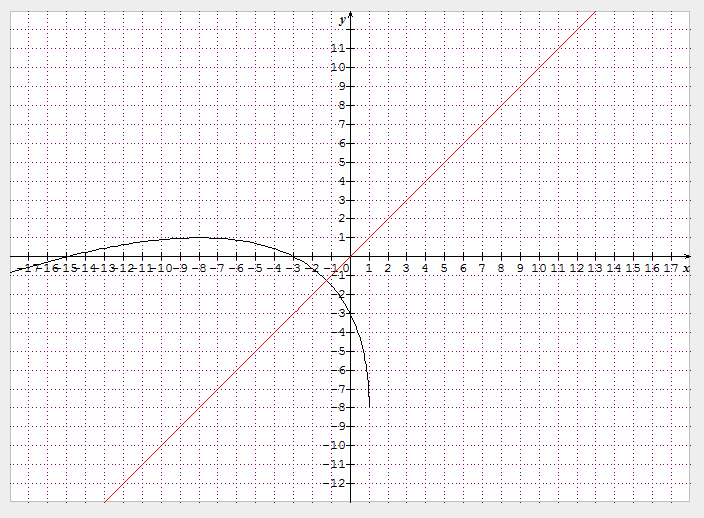
Voici le graphique de :

(graphique réalisé avec Sinequanon)

On voit bien que la fonction est symétrique sur le domaine de symétrie, et que pour les valeurs plus petites que , la symétrie n'existe plus parce que la valeur "maximale" de la fonction , et que pour les valeurs plus grandes que , la fonction n'existe pas.

En regardant le graphique, on remarque que la fonction répond à la définition mais seulement sur une partie de son domaine (le domaine d'existence des en fait). Si on applique de nouveau le théorème sur cette fonction, on va tomber sur une fonction encore moins symétrique, ce qui me pose problème.

Il y a sans doute une erreur quelque part dans ma démonstration qui fait des choses interdites ou "sous certaines conditions"...

Si quelqu'un qui a la bosse des maths pouvait m'aider, ce serait fort sympa,

En vous remerciant d'avance,

Aenonis
-----

[Jedoniuor]

Bonjour,

Votre démonstration générale me parait correcte. Ce qui ne va pas dans votre exemple de la racine carrée, c'est que la fonction n'est pas bijective de R dans R, donc n'admet pas de fonction inverse. La fonction racine carrée n'est définie que sur . Par contre, si vous prenez n impair, par exemple n=3, comme la racine n-ième est définie sur R, cela fonctionne parfaitement: vérifiez par exemple que la fonction racine cubique de est telle que .
Cordialement.

[Médiat]

Bonjour,

ainsi qu'une toute petite infinité

quand même !

Si on regarde la définition stricte, j'aurai pu m'arrêter là parce que, d'après moi, il n'en n'existait pas d'autres (cela demande vérification).

(en ajoutant et ), par exemple

[toothpick-charlie]

on peut imaginer des involutions non continues. Par exemple, en se limitant à [0,1[ l'application qui permute dans le développemt décimal d'un nombre la première et la deuxième décimale, la troisième et la quatrième, etc.

[A voir en vidéo sur Futura]

[Aenonis]

quand même !

Heu. Que signfie ce dans ta formule Médiat?

@Jedoniuor: ah oui, il faut, comme condition du théorème que soit complètement inversible donc complètement définie sur son domaine de définition afin de vérifier la définition, donc continue plus simplement.

Je n'avais pas pensé à ça, je te remercie !

@toothpick-charlie: ton message vient à moi comme du chinois... je m'explique, c'est quoi une involution non-continue? Sinon, le principe de l'application, je le comprends en tant que tel, je vois bien que ça correspond à la définition vu que la permutation de deux éléments, ben, si on les repermute, on revient à la situation initiale. Mais, je ne vois pas comment appliquer le théorème à ce genre de "fonction".

Au plaisir,

Aenonis

[Médiat]

Heu. Que signfie ce dans ta formule Médiat?

est le cardinal de IN,

est le cardinal de IR

[Aenonis]

Ah oui, je vois mieux, quand je dis, une petite infinité, c'est comparé à l'infinité infinie qui est gigantesque, et les fonctions de type ne sont qu'une partie infime de toutes les fonctions possibles et inimaginables, d'où mon adjectif "petite".

Amicalement,

Aenonis