Bonjour tout le monde!
Je me suis posé une question ce matin dont je n'arrive pas à répondre, ni d'ailleurs à trouver des informations sur internet.
Peut être que vous avez des idées?
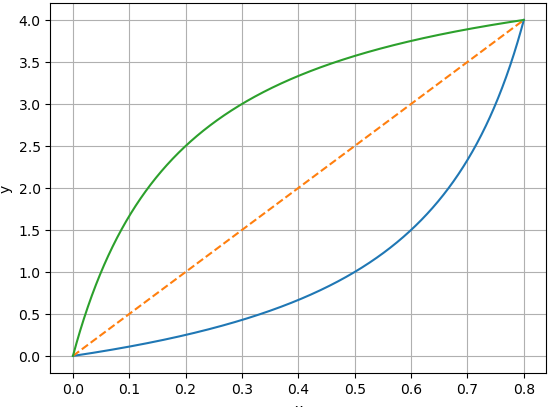
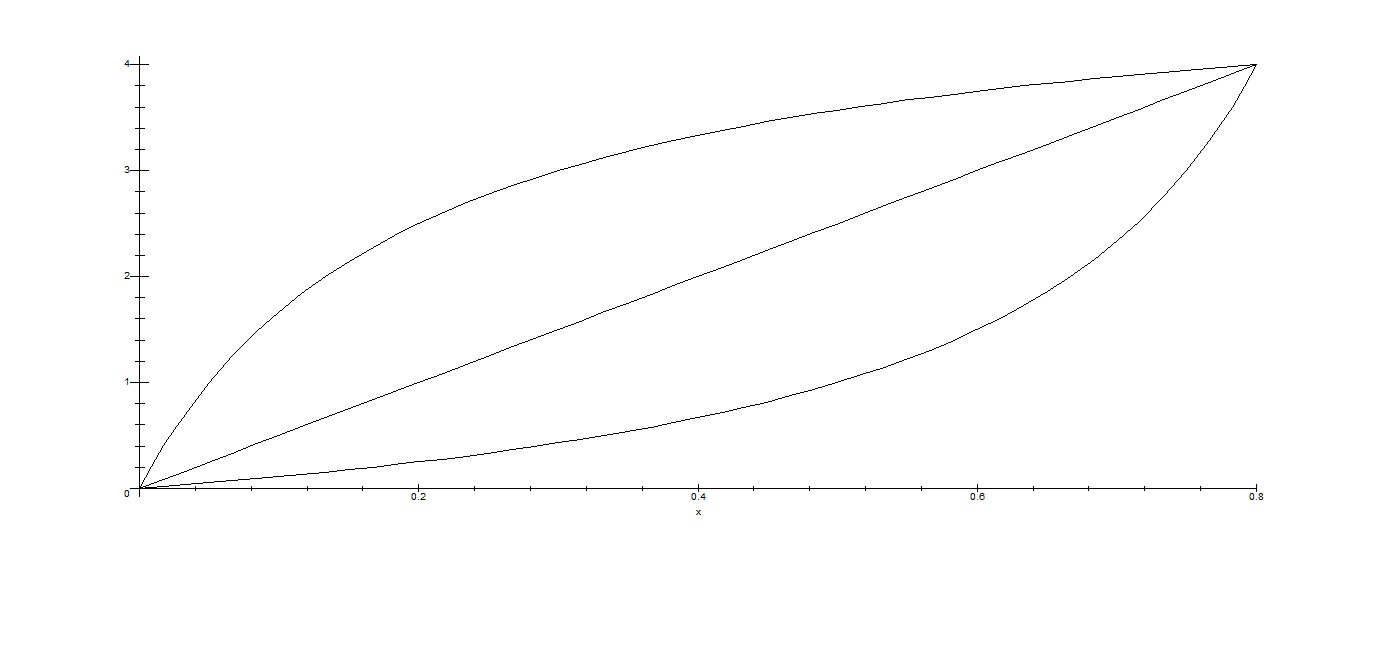
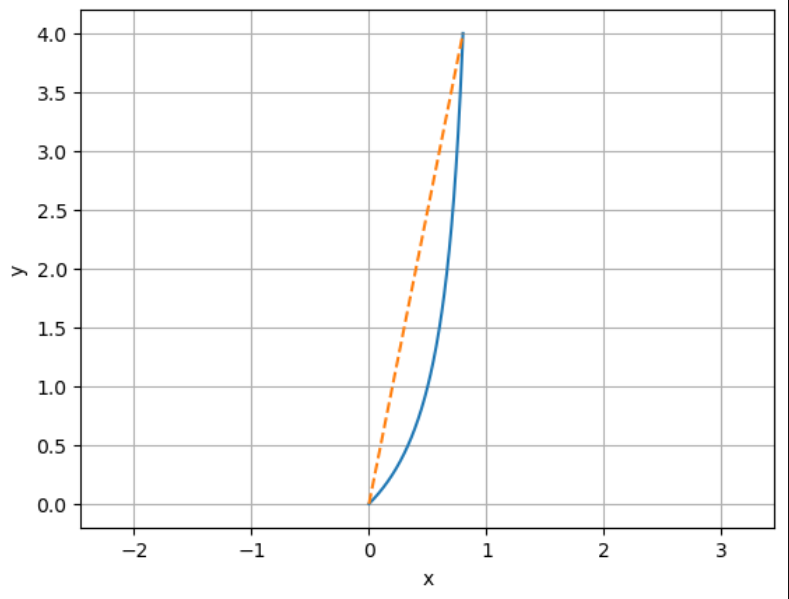
J'ai tracé la fonction en bleue: x/(1-x)
Maintenant, je souhaiterais tracer la "courbe symétrique" par rapport à la ligne orange. C'est facile de visualiser la symétrie ou de la dessiner.
Connaissant la fonction de départ, est elle possible de trouver la fonction qui correspond à la symétrie?
Est ce un problème compliqué a priori?
Merci à vous pour vos conseils et idées.
-----



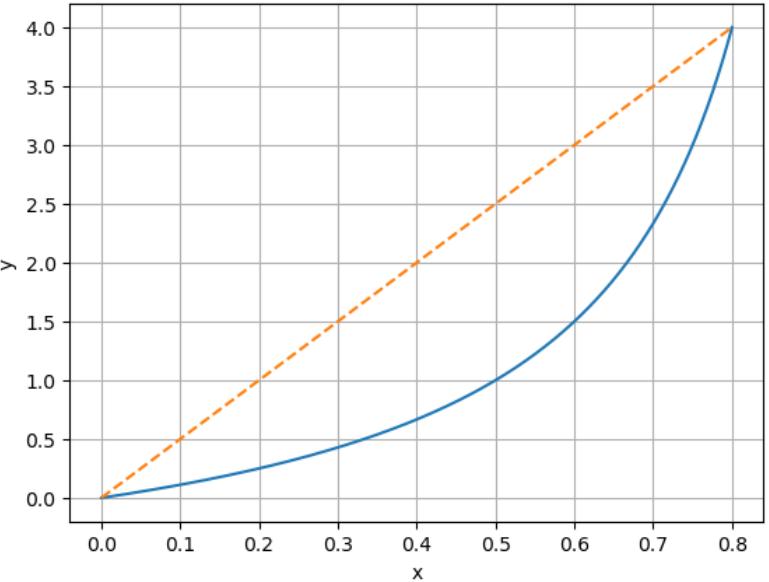
 est la courbe définie par la fonction inverse :
est la courbe définie par la fonction inverse :