Echange de chaleur avec le vide

[Gilgamesh]

Bonjour,

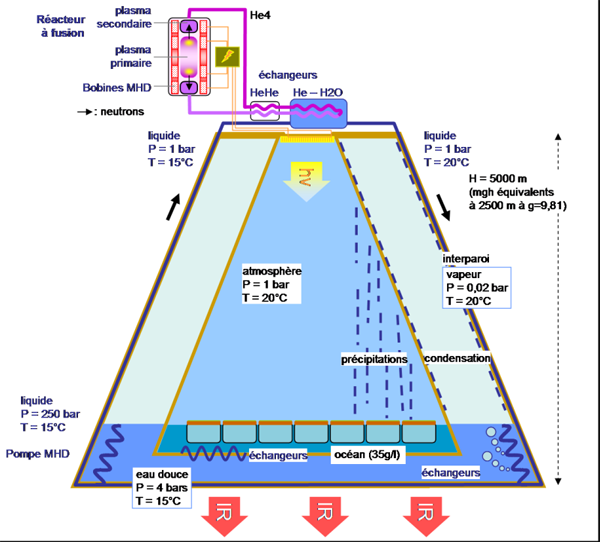
je voudrais poser proprement l'équation de diffusion de chaleur entre un milieu formé de vapeur d'eau saturée (température constante de 20°C à 0,2 bar) et le vide, à travers une parois où circule de l'eau.

Un petit schéma :



J'ai représenté un segment de parois, de dimension angulaire alpha (la paroi forme un disque évidé), à intégrer ensuite pour alpha = 2pi.

Les dimensions sont très grandes : R ~ 10 km.

La vitesse de circulation de l'eau dans la paroi est faible a priori, qq mm/s et le flux est laminaire. Mais elle n'est pas constante : u diminue de haut en bas.

A priori on va négliger l'effet de la pression croissante (haut à 1 bar, bas à 250 bars) sur les caractéristiques de l'eau (densité, conductivité thermique...).

L'épaisseur d'eau e ~ 1,5 m et celle des parois de part et d'autre p ~ 0,75 m environ. L'eau circule en fait dans des conduits circulaires mais je pense qu'on peut simplifier le problème comme je l'ai fait.

Au départ, à r=0, l'eau circulante est sans doute plus chaude que l'atmosphère saturée interne et le flux thermique est dans l'autre sens, mais on va considérer que la température interne est constante.

J'ai posé le problème ainsi :




Et déja je me dis que négliger la convection ne se justifie pas forcément


Est ce que quelqu'un pourrait m'aider à poser ça proprement, sur un segment dr du trajet, tenant compte de la vitesse décroissante du fluide ?


merci

a+
-----

[invite1c3dc18e]

le vide est un isolant thermique, on ne peut pas avoir d'échange de chaleur entre un objet et le vide absolu. On peut avoir communication d'énergie sous la forme de photons mais c'est tout.

Je ne saisis donc pas tout à fait ou tu veux en venir...

++

[f6bes]

Bjr Anacar.....
Ta réponse me chiffonne !!!
Ce qui veut dire (pas d'échange) qu'il n'y a pas de déperdition de chaleur entre, par exemple une SONDE INTERPLANETAIRE et le milieu dans lequel elle évolue (le vide). Ce qui ne pourrait conduire (pas d'échange) qu'à une élevation de température, au fil du temps, de la SONDE et à sa destruction par la chaleur que génére ses équipements.
Doit y avoir un hic qq part !

Gilgamech, j'ai détourné ton sujet, excuse m'en .De plus tu l'as bien compris, je ne serais d'aucun secours pour ta demande.
Cordialement

[Gilgamesh]

On peut avoir communication d'énergie sous la forme de photons mais c'est tout.

Et ça me suffit .

Comme tu peux voir, le dernier terme du flux de chaleur (fleche rouge) est radiatif, sous forme d'infra rouge :

Le vide c'est le vide spatial et d'ailleurs il faudrait que je précise la température de fond de rayonnement. Disons = 3 K ? C'est à retirer du :



Et sigma est une valeur qui prend en compte l'émissivité...

a+

[A voir en vidéo sur Futura]

[invite1c3dc18e]

Bjr Anacar.....
Ta réponse me chiffonne !!!
Ce qui veut dire (pas d'échange) qu'il n'y a pas de déperdition de chaleur entre, par exemple une SONDE INTERPLANETAIRE et le milieu dans lequel elle évolue (le vide). Ce qui ne pourrait conduire (pas d'échange) qu'à une élevation de température, au fil du temps, de la SONDE et à sa destruction par la chaleur que génére ses équipements.
Doit y avoir un hic qq part !

bonjour f6bes,

non parce que les équipements perdent de la "chaleur" (c'est de l'énergie plutôt, en thermo la chaleur est consacrée exclusivement pour décrire les transferts d'énergie par collisions entre atomes) principalement par rayonnement infra-rouge. D'ailleurs le problème principal tu le sens bien, c'est qu'un satellite sera aussi réchauffé par le soleil et aura des problèmes pour effectuer des échanges thermiques avec son environnement qu'il n'a pas Faudra qu'il soit le plus réfléchissant possible afin de ne pas s'échauffer.

Il réémettra donc des photons pour se refroidir. Bon maintenant les ordres de grandeur de tous ces phénomènes je ne les connais pas...

++

[obi76]

Il réémettra donc des photons pour se refroidir. Bon maintenant les ordres de grandeur de tous ces phénomènes je ne les connais pas...

Ils sont extrêmement élevés pour de l'électronique aussi précise (sur des plaques en or, malgré leur réflectivité la différence de température entre les 2 faces peut dépasser les 300/400 °C).
la technique utilisée est d'avoir des obturateurs sur le satellite pour faire rentrer plus ou moins de lumière dedans afin de "réguler" la température globale.

[Gilgamesh]

bonjour f6bes,

non parce que les équipements perdent de la "chaleur" (c'est de l'énergie plutôt, en thermo la chaleur est consacrée exclusivement pour décrire les transferts d'énergie par collisions entre atomes) principalement par rayonnement infra-rouge. D'ailleurs le problème principal tu le sens bien, c'est qu'un satellite sera aussi réchauffé par le soleil et aura des problèmes pour effectuer des échanges thermiques avec son environnement qu'il n'a pas Faudra qu'il soit le plus réfléchissant possible afin de ne pas s'échauffer.

Il réémettra donc des photons pour se refroidir. Bon maintenant les ordres de grandeur de tous ces phénomènes je ne les connais pas...

++

Ici on considère qu'on est *loin* du Soleil et toute autre source de rayonnement intense

Il s'agit d'une Arche interstellaire et le calcul concerne l'eau de refroidissement que l'on fait circuler dans les parois pour permettre à l'Arche d'évacuer ses calories.


Voici le circuit complet de production d'énergie, vu de profil (alors que le premier schéma de ce fil j'ai dessiné une vue "face paroi")




On s'intéresse à l'eau de refroidissement qui sort de l'échangeur hélium-eau et qui circule dans la paroi extérieure. Les flancs rayonnent comme le "plancher' (les IR partent "horizontalement" je sais pas si c'est bien clair).

Et en même temps qu'ils évacuent de la chaleur vers l'espace par rayonnement, ils forment une paroi froide permettant à la vapeur interparoi de se condenser et de précipiter.

On a donc plancher qui évacue un flux de chaleur correspondant au "soleil" interne (125 GW) + eau de condensation et les flancs qui évacuent la chaleur du circuit de refroidissement (90 GW environ, ça dépend du rendement).



a+