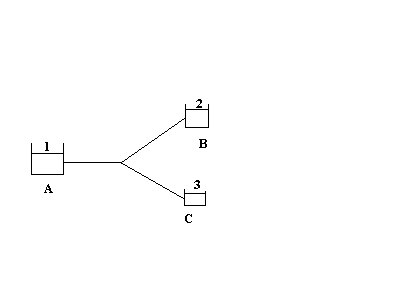
Bonsoir,
C’est au sujet du Théorème de Bernoulli.
Dans une configuration ou j’ai une conduite qui se divise en deux.
Comment puis-je l’appliquer ?
Puis-je l’appliquer séparément entre (1) et (2) puis (1) et (3) ?
Je me pose cette question car on a le droit d’appliquer Bernoulli sur une même ligne de courant ; la j’ai l’impression que ma ligne de courant se divise donc…. ?
oui pas de pb tant que tu restes dans le domaine d'application de Bernoulli.
dm
Donc je peux ecrire:Envoyé par dmeier
Ce qui m’embrouille c’est quand on dit sur « la même ligne de courant » ,
De ce fait doit-je imaginer qu’ la division ma ligne de courant poursuivra son chemin sur l’une des conduite seulement?
Merci.
Bonjour,
Oui, mais il ne faut pas oublier que Bernoulli est au fond le principe de conservation d’énergie. Donc, l’énergie volumique au point a se retrouvera dans l’ensemble des points b et c.
Il faut donc ajouter en plus la condition de conservation de la quantité de flux.
Le flux en a (Aa*va si on néglige les variation de pression) sera le flux total de b et c , soit (Ab * vb)+ (Ac * vc)
A: aire
Oups, je répondais à dmeir.
Bonsoir
Alors voila ; justement comme à la base Bernoulli c’est de la conservation d’énergie
J’aurais été tenté d’écrire que
Sinon je suis d’accord pour les flux : conservation du débit mais n’arrive pas à faire la liaison avec la conservation de l’énergie?
c'est une conservation volumique de l'énergie, tu dois appliquer B en considérant séparément les lignes, comme tu l'as fait au début. il ne faut pas sommer.
Comme le dit à juste titre mbochud, il faut tenir compte de la conservation du débit.
dm
j'ajouterais simplement qu'il manque un facteur 1/2 sur le terme d'énergie cinétique V²/2...
Oui, oui bien sur.
Je pourrais m’en tenir à l’application direct de ces lois, mais sincerement j’aurais bien aimé avoir quelques détails : ce qui nous permet d’opérer ainsi (le sens)?(cela ne me parait pas si évident!!)
POur le facteur 1/2 c'est bien vu, je me fais vieux...
POur répondre à mau13, l'énergie étant volumique on suit une particule élémentaire de fluide, donc quand une ligne de courant se sépare on suit deux particules de fluide différentes le long de chaque ligne.
La conservation de l'énergie sera assurée par les bornes de l'intégrale, c'est un peu pour ça qu'il ne faut pas faire de somme.
J'ai un peu aidé ?
dm
essaye de décrire le problème complètement comme ça on apportera plus d'indications......
C’est simplement que je me pose la question : D’où émane la possibilité d’appliquer Bernoulli respectivement entre (1) et (2) et (1) et (3).Rien de plus.
Oui merci pour cette apport dmeier, ça se tient (je n’avais pas pensé a réfléchir sur une particule élémentaire), ça rejoint un peu ce que je disais plus haut : à l’arrivé à l’embranchement cette particule élémentaire poursuivra son chemin sur l’une des conduites.
Ce qui fait qu’en appliquant Bernoulli entre (1) et (2) ou (1) et (3) nous avons considéré deux lignes de courants différentes (en quelque sorte supposé l’itineraire de deux particules élémentaire différentes)
eb bien en fait bernoulli s'énonce comme suit:
En mouvement permanent de fluide parfait (non visqueux) incompressible en présence de forces extérieures de volume dérivant d'un potentiel la quantité P+rhoV²/2 +rhogh reste constante sur tout une ligne de courant.
Tu as donc le droit de l'utiliser autant de fois sur toutes les lignes de courant que tu désires... Et tu écriras à la manière de ce que tu as écris dans ton deuxième message et pas dans ton troisième message ou tu ne respectes pas les règles imposées par bernoulli à savoir le long d'une meme ligne de courant, dans ton troisième message tu scindes en deux une ligne de courant et te retrouve sur deux lignes de courant diffférentes (bernoulli ne s'applique doc plus)
Oui, oui je pensais que c’était une linge de courant qui donner naissance à deux ligne de courants (à l’embranchement).C’est pour cela que j’ai sommer, mais comme l’a dit dmeier le raisonnement doit être fait sur une particule élémentaire, donc la je m’aperçoit vite que mon premier raisonnement été effectivement erroné.
Merci à tous ;
s'il y a des plus....
